Aritalab:Lecture/NetworkBiology/Zipf
From Metabolomics.JP
Contents |
Zipf の法則とランク・サイズ則
都市毎の人口や会社の規模、個人の所得を大きさの順に並べて順位 r をつけ、その大きさを 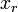 とおくと
とおくと
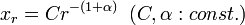
の形になります(α の値は小さい)。一般には Zipf の法則として知られる関係は、Rank-Size Rule とも呼ばれます。
ランダムな区画取り
ランダムに 2 点をとったとき、 2 点間の距離の分布
線分 [0,1] 上にランダムにとる点を 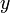 とします。一般性を失わずに
とします。一般性を失わずに 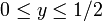 とします。
とします。 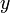 から距離 x と x + dx の間に 2 点目を取る確率を計算します。
から距離 x と x + dx の間に 2 点目を取る確率を計算します。
- 0 または 1 から幅 x 以内に
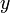 をとるとき
をとるとき
確率 2 x で 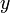 から x 離れた地点は片側にしかとることができません。2 番目の点が x と x + dx の間に落ちる確率は
から x 離れた地点は片側にしかとることができません。2 番目の点が x と x + dx の間に落ちる確率は 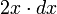 です。
です。
- 残りの範囲に
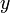 をとるとき
をとるとき
確率 1 - 2 x で 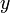 から x 離れた地点を両側にとることができます。2 番目の点が x と x + dx の間に落ちる確率は
から x 離れた地点を両側にとることができます。2 番目の点が x と x + dx の間に落ちる確率は 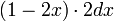 となります。
となります。
結局、2 点間の距離の確率は 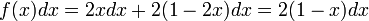 で与えられます。平均値は 1/3 になります。
で与えられます。平均値は 1/3 になります。
ランダムに 2 点をとる作業を n 回繰り返したとき、r 番目の距離の分布
ランダムにとった区間長が 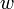 より長い確率 p 、短い確率 q はそれぞれ
より長い確率 p 、短い確率 q はそれぞれ
となります。n 回繰り返したときに、r 番目の区間長が 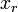 である期待値
である期待値 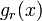 は
は 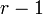 個が
個が 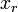 より短く、
より短く、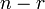 個が
個が 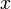 より長い区間を得ることに相当します。
より長い区間を得ることに相当します。
の期待値を計算するのに 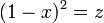 と変数変換します。
微分すると
と変数変換します。
微分すると 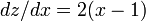 です。
です。
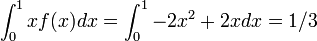
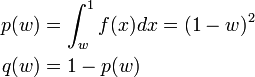
![\begin{align}
g_r(x) &= \frac{n!}{(n-r)!(r-1)!}p(x)^{r-1}q(x)^{n-r} f(x) \\
&= \frac{n!}{(n-r)!(r-1)!} (1 - x)^{2(r-1)}[1-(1 - x)^2]^{n-r} \cdot 2(1-x)
\end{align}](/mediawiki/images/math/2/1/a/21a5acc6a71f28b460b96f61ba6d9627.png)
![\begin{align}
\int^1_0 x g_r(x) dx &=
\frac{n!}{(n-r)!(r-1)!} \int^0_1 (1-z^{1/2}) z^{r-1}(1-z)^{n-r} \cdot 2(1-x) dz (dx/dz) \\
&= \frac{n!}{(n-r)!(r-1)!} \int^1_0 (1-z^{1/2}) z^{r-1}(1-z)^{n-r} dz \\
&= \frac{n!}{(n-r)!(r-1)!}\big[ \int^1_0 z^{r-1}(1-z)^{n-r} dz - \int^1_0 z^{r-1/2}(1-z)^{n-r} dz\big] \\
&= \frac{n!}{(n-r)!(r-1)!}\big[ \frac{\Gamma(r)\Gamma(n-r+1)}{\Gamma(n+1)} - \frac{\Gamma(r+\frac{1}{2})\Gamma(n-r+1)}{\Gamma(n+\frac{3}{2})} \big] \\
&= \frac{n!}{(n-r)!(r-1)!}\big[ \frac{(r-1)!(n-r)!}{n!} - \frac{\Gamma(r+\frac{1}{2})}{\Gamma(n+\frac{3}{2})} (n-r)! \big] \\
&= 1 - \frac{n!}{(r-1)!}\frac{\Gamma(r+\frac{1}{2})}{\Gamma(n+\frac{3}{2})}
\end{align}](/mediawiki/images/math/1/0/d/10d36055734f76df763a1a09881daf04.png)