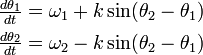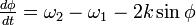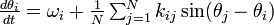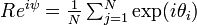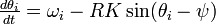Aritalab:Lecture/NetworkBiology/Coupled Oscillator
Contents |
系の安定性
一般的な 2 次元の系 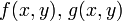 を考え、不動点を
を考え、不動点を 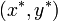 としましょう。
としましょう。
不動点に近い位置を 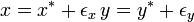 と書くと
と書くと
となります。関数 g についても同様です。これをヤコビ行列の形に書けば
です。ヤコビアンの簡単な場合として対角行列を考えましょう。
この解は以下のようになります。
x, y について書き直すと以下になります。
つまり 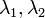 の値(それぞれ不動点における関数 f, g の微分値) が共に負であれば
の値(それぞれ不動点における関数 f, g の微分値) が共に負であれば 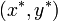 は誘引点、共に正であれば反発点、片方だけ負であれば鞍点 (saddle point) となります。
は誘引点、共に正であれば反発点、片方だけ負であれば鞍点 (saddle point) となります。
ヤコビアンが対角行列でない場合、行がヤコビアンの左固有ベクトルに対応する行列 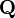 を用意し、
を用意し、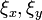 を定義します。
を定義します。
もし 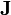 の固有ベクトルを求めることができれば
の固有ベクトルを求めることができれば 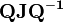 が対角行列になり、
が対角行列になり、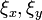 は互いに独立に時間発展することになります。
は互いに独立に時間発展することになります。
固有値が複素数になる場合 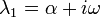 、一般解は指数的に増減する部分と振動する部分の積になります (C: 虚数, A, B: 実数)。
、一般解は指数的に増減する部分と振動する部分の積になります (C: 虚数, A, B: 実数)。
パラメータ α が負の場合は不動点に落ち込むスパイラル(安定点)になり、正の場合は不動点から遠ざかる不安定点です。一点に落ち込むことなく、安定した軌道を描く場合もあります。これをリミットサイクルと呼びます。
結合振動子
自然振動にばらつきのある素子が相互作用する系を考えましょう。 この分野で最も重要な貢献をした統計物理学者が 蔵本由紀 です。 同期のしやすさはネットワークの形状によりますが、ここでは最も簡単な場合として2個の振動子を考えます。
2つの振動子
振動子の振る舞いは以下の式で記述されます。
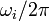 は i に固有の周波数です。また
は i に固有の周波数です。また 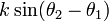 の部分は振動子どうしの引き込み項に対応し、位相の大きさによって周波数に影響を与えます。
周波数の差分
の部分は振動子どうしの引き込み項に対応し、位相の大きさによって周波数に影響を与えます。
周波数の差分 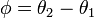 が
が 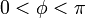 のとき(つまり振動子2が1より前にいるとき)は振動子1が加速して振動子2が減速し、逆に差分が
のとき(つまり振動子2が1より前にいるとき)は振動子1が加速して振動子2が減速し、逆に差分が 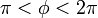 のときは振動子1が減速して振動子2が加速します。
のときは振動子1が減速して振動子2が加速します。
k (>0) が十分に大きければ振動子は同期、つまり共通の振動数をとって 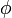 が安定します。
もし
が安定します。
もし 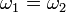 であれば k = 0 でも同期するため、一般性を失わずに
であれば k = 0 でも同期するため、一般性を失わずに 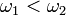 と仮定して、上式の差分を考えましょう。
と仮定して、上式の差分を考えましょう。
定常状態では 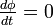 だから
だから
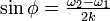 、つまり
、つまり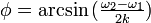 (
(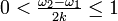 )
)
値 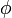 付近の振動子の振る舞いをみましょう。
関数
付近の振動子の振る舞いをみましょう。
関数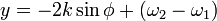 は正のy切片を持ち
は正のy切片を持ち 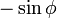 の波形を描きながら
の波形を描きながら 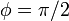 において極小値
において極小値 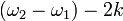 をとり、
をとり、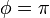 において正の値に戻ります。よって k の値によって以下の場合があります。
において正の値に戻ります。よって k の値によって以下の場合があります。
- k が大きく極小値が負の場合: 解を2つ持つ。そのうち
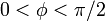 となるほうは振動子2が振動子1の前にある状態で、安定解となる。もう片方は不安定解になる。
となるほうは振動子2が振動子1の前にある状態で、安定解となる。もう片方は不安定解になる。
- k が適切な値で極小値が0の場合: 解を1つ持つ。この値は不安定解になる。
- k が0に近く、極小値が正の場合: 解を持たない。つまり定常状態が存在しない。
結論として、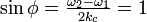 を満たす臨界値
を満たす臨界値 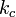 が存在し、この値より k が大きい場合は安定解
が存在し、この値より k が大きい場合は安定解 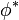 が存在します。
それと等しいか、小さい場合は安定解が存在せず、二つの振動子が同期することはありません。
が存在します。
それと等しいか、小さい場合は安定解が存在せず、二つの振動子が同期することはありません。
N個の振動子
振動子が N 個の場合は
結合する振動子どうしは 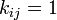 それ以外は 0 とします。
全ての振動子が同数だけ ( K とします) 結合するグラフの場合、
それ以外は 0 とします。
全ての振動子が同数だけ ( K とします) 結合するグラフの場合、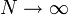 の極限において解くことができます(蔵本モデル)。
の極限において解くことができます(蔵本モデル)。
基本的なアイデアとして、集団としての振幅と位相をそれぞれ R (定数), ψ とおいて
平均化した近似を考えます(R = 定数)。このとき、振動子集団は見かけ上
と簡略化でき、定常状態では 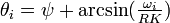 です。
です。
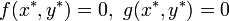
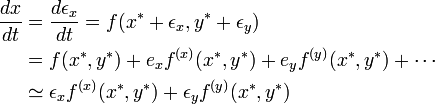
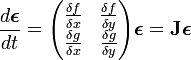
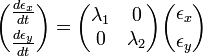
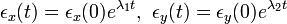
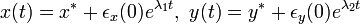
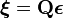
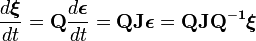
![\, \xi_1(t) = \mbox{Re}[ C e^{(\alpha+ i\omega)t}] = e^{\alpha t} (A \cos \omega t + B \sin \omega t)](/mediawiki/images/math/e/1/b/e1bebf14195e6593f6fed8aea5ec9e1d.png)