Aritalab:Lecture/Basic/Probability Generating Function

確率母関数

ある確率分布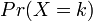$Pr(X=k)$の確率母関数(probability generating function または pgf)を以下のように定義する。

$\textstyle G_X(z) = \Sigma_{k=0}^{\infty}\mbox{Pr}(X=k)z^k$

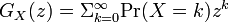
確率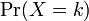$\mbox{Pr}(X=k)$は全て正の値でkについて全て足しあわせると1になる。

$\textstyle G_X(1) = \Sigma_{k=0}^{\infty}\mbox{Pr}(X=k)z^k = \Sigma_{k=0}^{\infty}\mbox{Pr}(X=k) = 1$

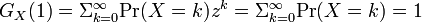
逆に係数が非負で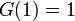$G(1) = 1$であるようなべき級数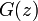$G(z)$があれば、それは何らかの確率母関数である。

平均と分散

確率母関数を使うと平均と分散の計算が容易にできる。

$\textstyle \begin{align} EX &= \Sigma_{k=0}^{\infty}k\mbox{Pr}(X=k) \\ &= \Sigma_{k=0}^{\infty}\mbox{Pr}(X=k) \cdot kz^{k-1} \bigg|_{x=1} \\ &= G_X'(1) \end{align}$

$\textstyle \begin{align} E(X^2) &= \Sigma_{k=0}^{\infty}k^2\mbox{Pr}(X=k) \\ &= \Sigma_{k=0}^{\infty}\mbox{Pr}(X=k) \cdot \big( k(k-1) z^{k-2} + kz^{k-1} \big) \bigg|_{x=1} \\ &= G_X''(1) + G_X'(1) \end{align}$

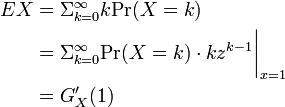
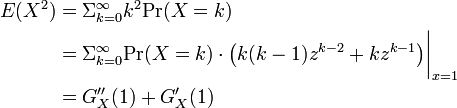
したがって

$\textstyle VX = G_X''(1) + G_X'(1) - G_X'(1)^2$