Aritalab:Lecture/Bioinformatics/Phylogeny

配列の進化

配列進化を考える際は、配列にランダムに変化が入るマルコフモデルを用います。配列の置換やギャップは出生死亡過程としてモデルします。

置換速度行列

一番単純なのは Junks-Cantor (JC) モデルで、全ての塩基が等確率で別の塩基に変化すると仮定します。

$R = \begin{bmatrix} - 3 \alpha & \alpha & \alpha & \alpha \\ \alpha & - \alpha & \alpha & \alpha \\ \alpha & \alpha & - \alpha & \alpha \\ \alpha & \alpha & \alpha & - \alpha \end{bmatrix}$

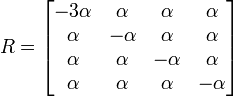
トランジションとトランスバージョン

プリン間 ( A ⇔ G )、ピリミジン間 ( C ⇔ T ) の置換を転位 (transition) とよび、それ以外の（つまりプリンとピリミジン間の）置換を転換 (transversion) と呼びます。転位のほうが起きやすい置換のため、これを反映させたのが木村資生による 2 変数モデルです。

$R = \begin{bmatrix} - 2 \beta - \alpha & \beta & \alpha & \beta \\ \beta & - 2 \beta - \alpha & \beta & \alpha \\ \alpha & \beta & - 2 \beta - \alpha & \beta \\ \beta & \alpha & \beta & - 2 \beta - \alpha \end{bmatrix}$

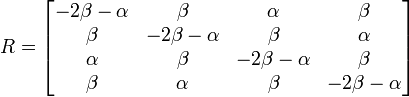
塩基の置換はアミノ酸の変更につながる場合があります。同じアミノ酸をコードするコドン間の置換を同義置換 (synonymous substitution)、そうでないものを非同義置換と呼びます。

進化系統樹

生物の進化にそった種分岐を樹状に表現したものが系統樹 (phylogenetic tree) です。樹の葉（末端部分）が現存する生物種にあたり、遡った頂点ほど祖先にあたる（現存しない）生物種を意味します。根つき (rooted) で描く方法と、根を仮定しない (unrooted) 方法があり、根を求めるには、対象とする生物種とおおきくかけ離れた種をひとつ加えます。これを外群 (outgroup) と呼び、この種と残りすべてを結ぶ頂点を根とみなします。

系統樹を作成するには、アライメント等で求めた配列間の距離から作る場合と、配列そのものを用いて作る場合の二通りがあります。

距離から作る場合

平均距離法 UPGMA

UPGMA は Unweighted Pair Group Method with Arithmetic Means の略です。複数生物種間の進化距離を与えられた時、以下の手順で系統樹を作成します。

1. 距離が最小のペア i, j を選ぶ （距離を d_i,j とします）
2. 生物種 i と j を、距離 d_i,j/ 2 に位置する分岐点 u を用いてつなぎ、この点を新しい種とみなす
3. 他の種 k からの距離を d_k,u = (d_k,i + d_k,j)/2 として再計算
4. このステップを全生物種がまとまるまで繰り返す

UPGMAは配列進化の速度が一定であると仮定しているため、各分岐点から葉頂点（各生物種）までの長さを揃えた有根系統樹を作成します。進化速度一定という仮定は正しいとは思えませんが、これはUPGMA法がタンパク質などの電気泳動パターンを分類するために開発された手法だからです。計算が早くて便利ですが、UPGMA法を系統樹の作成法として広めたのが良くなかったと思います。

近隣結合法 NJ

NJ は Neighbor Joining 法と呼ばれ、無根の進化系統樹を作成するために開発された手法です。

1. 各生物種 i に対し、他からの距離の総和 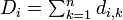$D_i = \textstyle \sum^n_{k=1} d_{i,k}$ を求める
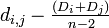2. $\textstyle d_{i,j} - \frac{(D_i + D_j)}{n-2}$ を最小にするペア i , j を選ぶ
3. 生物種 i と j を
     i から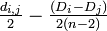 $\textstyle \frac{d_{i,j}}{2} - \frac{(D_i - D_j)}{2(n-2)}$
     j から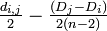 $\textstyle \frac{d_{i,j}}{2} - \frac{(D_j - D_i)}{2(n-2)}$ の分岐点 u を用いてつなぐ
4. 他の種 k からの距離を d_k,u = (d_k,i + d_k,j - d_i,j)/2 として再計算
5. このステップを全生物種がまとまるまで繰り返す

ステップ 2 の部分がわかりづらいですが、これは生物種全てで星状の系統樹を作ったときに一番中心に近い生物種を選んでいることに相当します。距離が近いものから順次つなぐために全枝長を最小にする系統樹が得られる保証はありませんが、実用上はこれで十分です。

配列を直接作る場合

最大節約法 MP

MP 法は maximum parsimony を意味し、最節約法とも呼ばれます。塩基の置換数を最低にするように、最尤法 (maximum likelihood method) で系統樹を作成します。計算時間が長いため、少数の配列についてしか適用できません。

ツール、ソフトウェア

• ナショナルバイオデータベースセンターによるツールの紹介 こちら

参考