Aritalab:Lecture/Math/PLS
From Metabolomics.JP
< Aritalab:Lecture | Math(Difference between revisions)
m (→PLS: Partial Least Squares) |
m (→PLS: Partial Least Squares) |
||
| Line 4: | Line 4: | ||
そこで、説明変量に対して最初に主成分分析を施し、そのスコアを利用して目的変量との重回帰分析をおこなう手法を主成分回帰 (principal component regression) と呼びます。 | そこで、説明変量に対して最初に主成分分析を施し、そのスコアを利用して目的変量との重回帰分析をおこなう手法を主成分回帰 (principal component regression) と呼びます。 | ||
| − | ==PLS: | + | ==PLS: Projection to Latent Structures== |
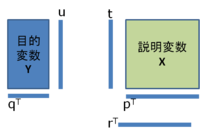
これまで、目的変量がひとつの場合だけを扱ってきましたが、目的変量側も数が多い場合に使うのがPLSです。 | これまで、目的変量がひとつの場合だけを扱ってきましたが、目的変量側も数が多い場合に使うのがPLSです。 | ||
Latest revision as of 09:54, 7 June 2017
[edit] 主成分回帰
回帰分析は説明変数間に相関が高いものがあると機能しませんでした(共線性の問題)。 そこで、説明変量に対して最初に主成分分析を施し、そのスコアを利用して目的変量との重回帰分析をおこなう手法を主成分回帰 (principal component regression) と呼びます。
[edit] PLS: Projection to Latent Structures
これまで、目的変量がひとつの場合だけを扱ってきましたが、目的変量側も数が多い場合に使うのがPLSです。 主成分回帰は説明変量側のみで主成分分析を施していましたが、同様の変量圧縮を目的変量側でもおこないます。以下では、目的変量と説明変量の行列が求めた主成分から構成されると仮定します。
[edit] NIPALSアルゴリズム
|
アルゴリズムのポイントは、Y側とX側の両方に対称に主成分回帰をおこなっている点です。