Aritalab:Lecture/NetworkBiology/Watts-Strogatz Model
From Metabolomics.JP
< Aritalab:Lecture | NetworkBiology(Difference between revisions)
m |
m |
||
| Line 3: | Line 3: | ||
=Watts-Strogatz Model= | =Watts-Strogatz Model= | ||
| − | 各頂点が<math>k</math> | + | 各頂点が<math>k</math>個の隣接点に接続した環状の格子グラフにおいて(総辺数は<math>kn/2</math>)、確率<math>p</math>で辺を張り直したものをWatts-Strogatzモデルという。辺を張りなおすモデルは解析が難しいので、環状の格子グラフにポアソン過程として<math>pkn/2</math>本の辺を追加するモデルがよく使われる。 |
==<math>p=0</math>のとき== | ==<math>p=0</math>のとき== | ||
| Line 11: | Line 11: | ||
1ステップで<math>k/2</math>点スキップでき、環状格子で一番離れている点は<math>n/2</math>なので、<math>L(0) \leq n / k</math>。 | 1ステップで<math>k/2</math>点スキップでき、環状格子で一番離れている点は<math>n/2</math>なので、<math>L(0) \leq n / k</math>。 | ||
==<math>p=1</math>のとき== | ==<math>p=1</math>のとき== | ||
| + | ランダムグラフと思えばよい。 | ||
| + | ;クラスター係数 | ||
| + | <math>k</math>辺を張りかえるとき、<math>n</math>頂点の中から<math>k</math>隣接点を選べばよいので<math>C(1) \simeq k/n</math>。 | ||
| + | ;平均頂点間距離 | ||
| + | 辺をランダムに張りかえるので<math>L(1) \simeq \log n / \log k</math>。 | ||
| + | |||
| + | ==一般の場合== | ||
Revision as of 12:10, 8 May 2009
Contents |
歴史と参考図書
- Watts DJ, Strogatz SH. "Collective dynamics of 'small-world' networks.". Nature 393 (6684):409–10, 1998. doi:10.1038/30918
Watts-Strogatz Model
各頂点が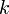 個の隣接点に接続した環状の格子グラフにおいて(総辺数は
個の隣接点に接続した環状の格子グラフにおいて(総辺数は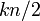 )、確率
)、確率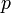 で辺を張り直したものをWatts-Strogatzモデルという。辺を張りなおすモデルは解析が難しいので、環状の格子グラフにポアソン過程として
で辺を張り直したものをWatts-Strogatzモデルという。辺を張りなおすモデルは解析が難しいので、環状の格子グラフにポアソン過程として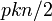 本の辺を追加するモデルがよく使われる。
本の辺を追加するモデルがよく使われる。
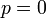 のとき
のとき
- クラスター係数
簡単のため左右の隣接点に同じ本数リンクを張ると仮定し、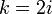 とする。注目する点を原点とした
とする。注目する点を原点とした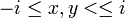 のxy座標系を考えたとき、
のxy座標系を考えたとき、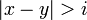 に対応する座標点は三角形
に対応する座標点は三角形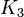 を形成せず、残りは形成する。その割合を考えると
を形成せず、残りは形成する。その割合を考えると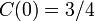 。
。
- 平均頂点間距離
1ステップで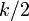 点スキップでき、環状格子で一番離れている点は
点スキップでき、環状格子で一番離れている点は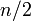 なので、
なので、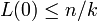 。
。
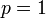 のとき
のとき
ランダムグラフと思えばよい。
- クラスター係数
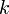 辺を張りかえるとき、
辺を張りかえるとき、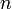 頂点の中から
頂点の中から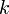 隣接点を選べばよいので
隣接点を選べばよいので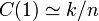 。
。
- 平均頂点間距離
辺をランダムに張りかえるので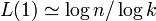 。
。