Sandbox
From Metabolomics.JP
(Difference between revisions)
m |
m |
||
| (2 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | ==根基イデアルとイデアル多様体対応== | |
| + | イデアルとアフィン多様体の対応は1対1ではない。 | ||
| + | 例えば <x> と <x<sup>2</sup>> は k[x] の異なるイデアルだが、多様体は同じである '''V'''(x) = '''V'''(x<sup>2</sup>) = { 0 } 。 | ||
| + | 体 k が代数的閉体でない場合、複素数解が生じる多項式は対応する多様体が空集合になってしまう。しかし代数的閉体である場合は k[x] の多項式は必ず根を持ち、空集合に対応するイデアルが複数にならず、'''V'''(I) = { } となるには多項式環全体つまり I = k[x] となる。これを示したのがヒルベルトの零点定理であった。 | ||
| − | + | §2では零点定理をイデアルの言葉で書きなおしてみる。 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | {{ | + | 零点定理によるとイデアル I が '''V'''(I) で消える多項式全体のなすイデアルとならない唯一の理由は、 I に含まれない多項式 f のベキ f<sup>m</sup> が I に含まれるからであった。そこで根基イデアルという概念を導入する。 |
| + | |||
| + | ;定義：ある整数 m に対しf<sup>m</sup>∈ I ならば f ∈ I を満たすとき、 I を根基 (radical) イデアルという。また、イデアル I に対してある整数 m があり f<sup>m</sup> ∈ I となる関数 f の集合を、イデアルの根基といって √I と記す。 | ||
| + | |||
| + | 定義における整数 m は 1 でもよいので、明らかに I ⊂ √I である。しかし I ≠ √I はありえる。例えばイデアル J = < x<sup>2</sup>, y<sup>3</sup> > ⊂ k[x,y] を考えよう。 x , y は J に属さないが x ∈ √J, y ∈ √J である。 (xy)<sup>2</sup> ∈ J から、xy ∈ √J 、さらに x + y ∈ √J である。しかし xy や x+y は J には属さないので、J ⊂ √J である。 | ||
| + | |||
| + | ;補題： I が k[x ...] のイデアルなら、 √I もイデアルになる。 | ||
| + | : f , g ∈ √I なら f<sup>m</sup>, g<sup>l</sup> ∈ I となる。そこで (f + g)<sup>m+l-1</sup>の2項展開を考えると 各項は f<sup>i</sup>g<sup>j</sup> を含んでいる(ただし i+j = m+l-1 ) 。このとき f<sup>i</sup> または g<sup>j</sup> のいずれかが I に含まれるので (f + g)<sup>m+l-1</sup> ∈ I になる。つまり (f + g) ∈ √I。 また同様に f ∈ √I なら hf ∈ √I となるので √I はイデアルである。さらに√Iは根基イデアルである。 | ||
| + | |||
| + | |||
| + | ;強形の零点定理 k を代数的閉体とする。 I を k[x, ...] のイデアルとすると、'''I'''('''V'''(I) ) = √Iとなる。 | ||
| + | :f ∈ √I とすると f<sup>m</sup> ∈I であり '''V'''(I) で消える。このとき f も消えるから f ∈ '''I'''('''V'''(I))。 | ||
| + | :逆に f ∈ '''I'''('''V'''(I)) のとき、f は '''V'''(I) で消えるから、零点定理よりある整数 m に対して f<sup>m</sup> ∈ I。すなわち f ∈ √I となる。 | ||
| + | |||
| + | ;定理（イデアル多様体対応） | ||
| + | :(i) アフィン多様体 → イデアル と、イデアル → アフィン多様体 は包含関係が逆になる。つまりイデアルが I<sub>1</sub> ⊂ I<sub>2</sub> なら、'''V'''(I<sub>1</sub>) ⊃ '''V'''(I<sub>2</sub>) になる。また多様体が V<sub>1</sub> ⊂ V<sub>2</sub> なら、'''I'''(V<sub>1</sub>) ⊃ '''I'''(V<sub>2</sub>) になる。また任意の多様体に対し '''V'''('''I'''(V)) = V となって'''I'''は常に1対1である。 | ||
| + | :(ii) k が代数的閉体の場合、根基イデアルだけを考えると上記の写像は互いに逆写像となる全単射である。 | ||
| + | |||
| + | 以上から、多様体に関する問題は根基イデアルに関する代数の問題に言い換えられる。イデアルに対し、次の3つの問が考えられる。 | ||
| + | * 根基の生成元: √I = <g, ...> となるような多項式の集合を生成するアルゴリズム ... 実用的でないものはHermann(1926)により示され、Gianni et al (1988)らにより数式処理システムに組み込まれたものが示された | ||
| + | * 根基イデアル: I が根基かどうかの判定アルゴリズム ... Gianni et al (1988)らにより数式処理システムに組み込まれたものが示された | ||
| + | * 根基所属: 与えられた多項式 f が f ∈ √I かどうかの判定アルゴリズム ... ここで解説 | ||
| + | |||
| + | イデアル I = <f, ...> を与えられた時、多項式 f が f ∈ √I であるかをみるには、I' = <f, ..., 1-yf> に定数多項式 1 が含まれるかどうかを判定するだけで良い。なぜなら | ||
| + | <math>\begin{align} | ||
| + | 1 = y^m f^m + (1 - y^m f^m ) = y^m f^m + (1 - yf)(1 + ...) | ||
| + | \end{align}</math> | ||
| + | であるから、もし 1 ∈ I' なら f<sup>m</sup> ∈ I を意味している。 また f ∈ √I ならある m に対して f<sup>m</sup> ∈ I を満たすから、1 ∈ I' となるため、 f ∈ √I の判定の必要十分条件になっている。 | ||
| + | |||
| + | このことは、適当な順序で I' = <f, ..., 1-yf> の簡約グレブナ基底を計算し、その結果が { 1 } であれば f ∈ √I, そうでなければ含まれないという結論になる。 | ||
| + | |||
| + | ;例 | ||
| + | : k[x,y] のイデアル <math> I = \langle xy^2 + 2 y^2 , x^4 - 2x^2 + 1> \rangle </math> に <math> f = y - x^2 + 1 </math> が所属するか判定する | ||
| + | : k[x,y,z] の lex 順序で | ||
| + | <math> I' = \langle xy^2 + 2y^2, x^4 - 2x^2 + 1, 1 - z(y - x^2 + 1)\rangle \subset k[x,y,z]</math> | ||
| + | は簡約グレブナ規定 { 1 } を持つ。よって <math> f = y - x^2 + 1 \isin \sqrt{I} </math> 。 | ||
Latest revision as of 14:56, 22 April 2013
[edit] 根基イデアルとイデアル多様体対応
イデアルとアフィン多様体の対応は1対1ではない。 例えば <x> と <x2> は k[x] の異なるイデアルだが、多様体は同じである V(x) = V(x2) = { 0 } 。 体 k が代数的閉体でない場合、複素数解が生じる多項式は対応する多様体が空集合になってしまう。しかし代数的閉体である場合は k[x] の多項式は必ず根を持ち、空集合に対応するイデアルが複数にならず、V(I) = { } となるには多項式環全体つまり I = k[x] となる。これを示したのがヒルベルトの零点定理であった。
§2では零点定理をイデアルの言葉で書きなおしてみる。
零点定理によるとイデアル I が V(I) で消える多項式全体のなすイデアルとならない唯一の理由は、 I に含まれない多項式 f のベキ fm が I に含まれるからであった。そこで根基イデアルという概念を導入する。
- 定義：ある整数 m に対しfm∈ I ならば f ∈ I を満たすとき、 I を根基 (radical) イデアルという。また、イデアル I に対してある整数 m があり fm ∈ I となる関数 f の集合を、イデアルの根基といって √I と記す。
定義における整数 m は 1 でもよいので、明らかに I ⊂ √I である。しかし I ≠ √I はありえる。例えばイデアル J = < x2, y3 > ⊂ k[x,y] を考えよう。 x , y は J に属さないが x ∈ √J, y ∈ √J である。 (xy)2 ∈ J から、xy ∈ √J 、さらに x + y ∈ √J である。しかし xy や x+y は J には属さないので、J ⊂ √J である。
- 補題： I が k[x ...] のイデアルなら、 √I もイデアルになる。
- f , g ∈ √I なら fm, gl ∈ I となる。そこで (f + g)m+l-1の2項展開を考えると 各項は figj を含んでいる(ただし i+j = m+l-1 ) 。このとき fi または gj のいずれかが I に含まれるので (f + g)m+l-1 ∈ I になる。つまり (f + g) ∈ √I。 また同様に f ∈ √I なら hf ∈ √I となるので √I はイデアルである。さらに√Iは根基イデアルである。
- 強形の零点定理 k を代数的閉体とする。 I を k[x, ...] のイデアルとすると、I(V(I) ) = √Iとなる。
- f ∈ √I とすると fm ∈I であり V(I) で消える。このとき f も消えるから f ∈ I(V(I))。
- 逆に f ∈ I(V(I)) のとき、f は V(I) で消えるから、零点定理よりある整数 m に対して fm ∈ I。すなわち f ∈ √I となる。
- 定理（イデアル多様体対応）
- (i) アフィン多様体 → イデアル と、イデアル → アフィン多様体 は包含関係が逆になる。つまりイデアルが I1 ⊂ I2 なら、V(I1) ⊃ V(I2) になる。また多様体が V1 ⊂ V2 なら、I(V1) ⊃ I(V2) になる。また任意の多様体に対し V(I(V)) = V となってIは常に1対1である。
- (ii) k が代数的閉体の場合、根基イデアルだけを考えると上記の写像は互いに逆写像となる全単射である。
以上から、多様体に関する問題は根基イデアルに関する代数の問題に言い換えられる。イデアルに対し、次の3つの問が考えられる。
- 根基の生成元: √I = <g, ...> となるような多項式の集合を生成するアルゴリズム ... 実用的でないものはHermann(1926)により示され、Gianni et al (1988)らにより数式処理システムに組み込まれたものが示された
- 根基イデアル: I が根基かどうかの判定アルゴリズム ... Gianni et al (1988)らにより数式処理システムに組み込まれたものが示された
- 根基所属: 与えられた多項式 f が f ∈ √I かどうかの判定アルゴリズム ... ここで解説
イデアル I = <f, ...> を与えられた時、多項式 f が f ∈ √I であるかをみるには、I' = <f, ..., 1-yf> に定数多項式 1 が含まれるかどうかを判定するだけで良い。なぜなら
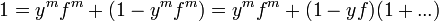であるから、もし 1 ∈ I' なら fm ∈ I を意味している。 また f ∈ √I ならある m に対して fm ∈ I を満たすから、1 ∈ I' となるため、 f ∈ √I の判定の必要十分条件になっている。
このことは、適当な順序で I' = <f, ..., 1-yf> の簡約グレブナ基底を計算し、その結果が { 1 } であれば f ∈ √I, そうでなければ含まれないという結論になる。
- 例
- k[x,y] のイデアル
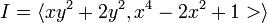に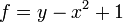 
が所属するか判定する
- k[x,y,z] の lex 順序で
![I' = \langle xy^2 + 2y^2, x^4 - 2x^2 + 1, 1 - z(y - x^2 + 1)\rangle \subset k[x,y,z]](/mediawiki/images/math/0/c/f/0cfd3164d37f05e888b50c0bc8636ff9.png)
は簡約グレブナ規定 { 1 } を持つ。よって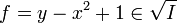 
。
