Aritalab:Lecture/NetworkBiology/Zipf
m (→ランダムな分割) |
m (→線分を s 個に分割する場合) |
||
| Line 77: | Line 77: | ||
==ランダムな分割== | ==ランダムな分割== | ||
| − | ===線分を s | + | ===線分を s 個に分割したときの長さの期待値=== |
線分 [0,1] をランダムに s 分割するとき、得られる線分の長さを短いものから長いものに並べ替えて <math>l_1, l_2, \cdots, l_s</math> と書きましょう。ここで <math>l_1< l_2 < \cdots < l_s </math> また <math>\textstyle \sum^s_{i=1} l_i =1</math> です。 | 線分 [0,1] をランダムに s 分割するとき、得られる線分の長さを短いものから長いものに並べ替えて <math>l_1, l_2, \cdots, l_s</math> と書きましょう。ここで <math>l_1< l_2 < \cdots < l_s </math> また <math>\textstyle \sum^s_{i=1} l_i =1</math> です。 | ||
Revision as of 09:37, 21 July 2011
Contents |
Zipf の法則とランク・サイズ則
都市毎の人口や会社の規模、個人の所得を大きさの順に並べて順位 r をつけ、その大きさを 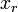 とおくと
とおくと
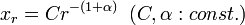
の形になります(α の値は小さい)。一般には Zipf の法則として知られる関係は、Rank-Size Rule とも呼ばれます。
ランダムな区画取り
ランダムに 2 点をとったとき、 2 点間の距離の分布
線分 [0,1] 上にランダムにとる点を y とします。一般性を失わずに 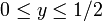 とします。 y から距離 x と x + dx の間に 2 点目を取る確率を計算します。
とします。 y から距離 x と x + dx の間に 2 点目を取る確率を計算します。
- 0 または 1 から幅 x 以内に
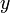 をとるとき
をとるとき
確率 2 x で 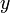 から x 離れた地点は片側にしかとることができません。2 番目の点が x と x + dx の間に落ちる確率は
から x 離れた地点は片側にしかとることができません。2 番目の点が x と x + dx の間に落ちる確率は 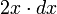 です。
です。
- 残りの範囲に
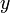 をとるとき
をとるとき
確率 1 - 2 x で 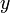 から x 離れた地点を両側にとることができます。2 番目の点が x と x + dx の間に落ちる確率は
から x 離れた地点を両側にとることができます。2 番目の点が x と x + dx の間に落ちる確率は 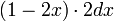 となります。
となります。
結局、2 点間の距離の確率は 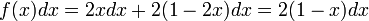 で与えられます。平均値は 1/3 になります。
で与えられます。平均値は 1/3 になります。
ランダムに 2 点をとる作業を n 回繰り返したとき、r 番目の距離の分布
ランダムにとった区間長が 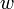 より長い確率 p 、短い確率 q はそれぞれ
より長い確率 p 、短い確率 q はそれぞれ
となります。n 回繰り返したときに、r 番目の区間長が 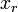 である確率
である確率 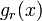 は
は 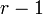 個が
個が 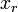 より短く、
より短く、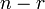 個が
個が 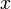 より長い区間を得ることに相当します。
より長い区間を得ることに相当します。
期待値を計算するのに 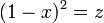 と変数変換します。
微分すると
と変数変換します。
微分すると 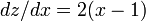 です。
です。
一番長い区間の期待値
一番短い区間の期待値
ランダムな分割
線分を s 個に分割したときの長さの期待値
線分 [0,1] をランダムに s 分割するとき、得られる線分の長さを短いものから長いものに並べ替えて 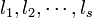 と書きましょう。ここで
と書きましょう。ここで 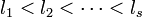 また
また 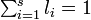 です。
です。
ここで r 番目の線分と r+1 番目の線分の差を 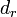 と書きます。
と書きます。
このとき 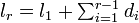 です。全ての線分を足し合わせると長さは 1 になります。
です。全ての線分を足し合わせると長さは 1 になります。
ここで全ての線分は等しい仮定の下に置かれていて期待値が等しいことを利用します[1][2]。
ここから
初めに仮定した l の形に戻しましょう。
同様に長いほうから順番に並べた場合は i 番目の長さは
以上をまとめます。
- 各線分の長さの期待値
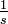
- 一番短い線分の期待値
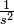
- 一番長い線分の期待値
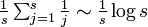
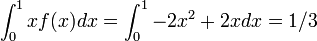
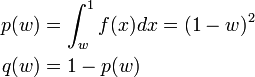
![\begin{align}
g_r(x) &= \frac{n!}{(n-r)!(r-1)!}p(x)^{r-1}q(x)^{n-r} f(x) \\
&= \frac{n!}{(n-r)!(r-1)!} (1 - x)^{2(r-1)}[1-(1 - x)^2]^{n-r} \cdot 2(1-x)
\end{align}](/mediawiki/images/math/2/1/a/21a5acc6a71f28b460b96f61ba6d9627.png)
![\begin{align}
E[g_r(x)] &= \int^1_0 x g_r(x) dx\\
&= \frac{n!}{(n-r)!(r-1)!} \int^0_1 (1-z^{1/2}) z^{r-1}(1-z)^{n-r} \cdot 2(1-x) dz (dx/dz) \\
&= \frac{n!}{(n-r)!(r-1)!} \int^1_0 (1-z^{1/2}) z^{r-1}(1-z)^{n-r} dz \\
&= \frac{n!}{(n-r)!(r-1)!}\big[ \int^1_0 z^{r-1}(1-z)^{n-r} dz - \int^1_0 z^{r-1/2}(1-z)^{n-r} dz\big] \\
&= \frac{n!}{(n-r)!(r-1)!}\big[ \frac{\Gamma(r)\Gamma(n-r+1)}{\Gamma(n+1)} - \frac{\Gamma(r+\frac{1}{2})\Gamma(n-r+1)}{\Gamma(n+\frac{3}{2})} \big] \\
&= \frac{n!}{(n-r)!(r-1)!}\big[ \frac{(r-1)!(n-r)!}{n!} - \frac{\Gamma(r+\frac{1}{2})}{\Gamma(n+\frac{3}{2})} (n-r)! \big] \\
&= 1 - \frac{n!}{(r-1)!}\frac{\Gamma(r+\frac{1}{2})}{\Gamma(n+\frac{3}{2})}
\end{align}](/mediawiki/images/math/7/1/f/71fb00f40ac1572866540a0709d2ce74.png)
![\begin{align}
E[g_1(x)] &= 1 - n! \cdot \frac{\Gamma(3/2)}{\Gamma((n+1)+ 1/2)} \\
&= 1 - \frac{ 2^{2n+1} n! (n+1)!}{(2n + 2)!}\\
\end{align}](/mediawiki/images/math/a/f/f/affe0c4c7070770f592ceb121333649c.png)
![\begin{align}
E[g_n(x)] &= 1 - n \cdot \frac{\Gamma(n+\frac{1}{2})}{\Gamma(n+\frac{3}{2})}\\
&= 1 - \frac{2n}{2n+1}
\end{align}](/mediawiki/images/math/d/4/7/d472faa6c8d6cd01256ec50f98e3c2be.png)
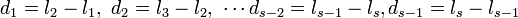
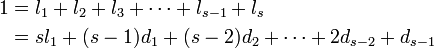
![\textstyle
E[sl_1] = E[(s-1)d_1] = E[(s-2)d_2] = \cdots = E[d_{s-1}] = \frac{1}{s}](/mediawiki/images/math/4/f/a/4fae007bb24f0a2e5c0a2fbf437b6c70.png)
![\textstyle
E[l_1] = \frac{1}{s^2},\ E[d_1] = \frac{1}{s(s-1)},\ E[d_2] = \frac{1}{s(s-2)},\ \cdots E[d_i] = \frac{1}{s(s-i)},\ \cdots E[d_{s-1}] = \frac{1}{s}](/mediawiki/images/math/6/8/4/6849649d70c2293014f489e3ce459c96.png)
![\begin{align}
E[l_2] &= \textstyle l_1 + d_1 = \frac{1}{s^2} + \frac{1}{s(s-1)}\\
E[l_3] &= \textstyle l_1 + d_1 + d_2 = \frac{1}{s^2} + \frac{1}{s(s-1)} + \frac{1}{s(s-2)}\\
\cdots \\
E[l_i] &= \textstyle \frac{1}{s}\sum^{i-1}_{j=0}\frac{1}{s-j}
\end{align}](/mediawiki/images/math/a/c/c/acc4b58fac23870494eecd8063b6463d.png)
![\textstyle
E[l_i] = \frac{1}{s}\sum^{s-i}_{j=0}\frac{1}{s-j}](/mediawiki/images/math/c/7/e/c7ef51b6b56080100dbfa7e76e0a982b.png)