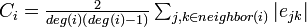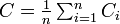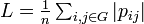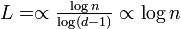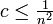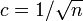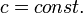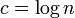Aritalab:Lecture/NetworkBiology/Erdos-Renyi Model
m (Draft:Erdős–Rényi moved to Draft:Erdos-Renyi) |
m |
||
| Line 1: | Line 1: | ||
ここでは頂点がすべて連結した無向グラフを扱う。 | ここでは頂点がすべて連結した無向グラフを扱う。 | ||
| − | = | + | =歴史と参考図書= |
| − | * | + | * Erdős P, Rényi A. "On Random Graphs. I.". Publicationes Mathematicae 6:290–297, 1959 |
| + | * Erdős P, Rényi A. "The Evolution of Random Graphs". Magyar Tud. Akad. Mat. Kutató Int. Közl. 5:17–61, 1960 | ||
| + | * Bollobás B. Random Graphs (2nd ed.), Cambridge University Press, 2001 | ||
| + | * Durrett R. Random Graph Dynamics, Cambridge University Press, 2004 | ||
=ネットワークの指標:<math>C</math>と<math>L</math>= | =ネットワークの指標:<math>C</math>と<math>L</math>= | ||
| Line 45: | Line 48: | ||
;<math>\textstyle c = const.</math> | ;<math>\textstyle c = const.</math> | ||
| − | 各頂点が定数本の辺を持ちはじめる。ちょうど1本だけだと二部グラフのマッチング、2本だと閉路の集合になる。各頂点が持つ辺の本数(の期待値)が<math>c</math>なので、<math>c < 1</math>のとき連結しても大きさは高々<math>\log n</math>程度にしかならない。しかし<math>c > 1</math>の場合繋がっていく確率のほうが高く、その半径(diameter)を<math>k</math>とおくと<math>c^k=n</math>まで成長する。このとき<math>k=\log n / \log c</math> | + | 各頂点が定数本の辺を持ちはじめる。ちょうど1本だけだと二部グラフのマッチング、2本だと閉路の集合になる。各頂点が持つ辺の本数(の期待値)が<math>c</math>なので、<math>c < 1</math>のとき連結しても大きさは高々<math>\log n</math>程度にしかならない。しかし<math>c > 1</math>の場合繋がっていく確率のほうが高く、その半径(diameter)を<math>k</math>とおくと<math>c^k=n</math>まで成長する。このとき<math>k=\log n / \log c</math>。臨界点にあたる<math>c = 1</math>では連結した頂点のサイズが<math>n^{2/3}</math>になることが知られている。 |
;<math>\textstyle c = \log n</math> | ;<math>\textstyle c = \log n</math> | ||
Revision as of 11:07, 8 May 2009
ここでは頂点がすべて連結した無向グラフを扱う。
Contents |
歴史と参考図書
- Erdős P, Rényi A. "On Random Graphs. I.". Publicationes Mathematicae 6:290–297, 1959
- Erdős P, Rényi A. "The Evolution of Random Graphs". Magyar Tud. Akad. Mat. Kutató Int. Közl. 5:17–61, 1960
- Bollobás B. Random Graphs (2nd ed.), Cambridge University Press, 2001
- Durrett R. Random Graph Dynamics, Cambridge University Press, 2004
ネットワークの指標: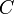 と
と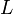
ネットワーク全体についての尺度として、クラスター係数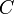 と平均頂点間距離
と平均頂点間距離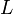 を紹介する。
を紹介する。
クラスター係数
クラスター係数は隣接する頂点間の辺の密度の平均値にあたる。まず各頂点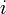 におけるクラスター係数
におけるクラスター係数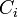 を以下のように定義する。辺の長さはすべて1とする
を以下のように定義する。辺の長さはすべて1とする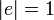 。
。
グラフ全体のクラスター係数はその平均値になる。
平均頂点間距離
平均頂点間距離はその字のごとく全頂点間の最短路の平均値にあたる。ここでは頂点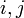 間の最短経路を
間の最短経路を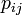 と書く。各点に注目する場合は、距離
と書く。各点に注目する場合は、距離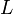 以内にある頂点数を数えることで求められる。
以内にある頂点数を数えることで求められる。
様々なグラフにおける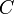 と
と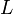
完全グラフ
全ての頂点間に辺を持つグラフは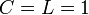 。
。
格子
平面の場合は三角格子、正方格子が考えられる。特に、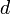 次元空間において辺の長さが単位距離の格子をZdと書く。
次元空間において辺の長さが単位距離の格子をZdと書く。
- 例. Z2において、
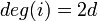
定義のままだとクラスター係数が0になって面白くないので、最短距離が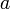 以下の点には全て辺を張るバリエーションZ'dを考えよう。
以下の点には全て辺を張るバリエーションZ'dを考えよう。
- 例. Z'dのクラスター係数は
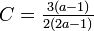 、平均頂点間距離は
、平均頂点間距離は![\textstyle L=\sqrt[d]{n}/a](/mediawiki/images/math/f/5/8/f583b41db535b1a73d0d831b87ea2808.png)
木
簡単のため全頂点が同じ次数を持つ木を考える。中心の頂点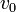 を根(root)と呼ぶ。木はその定義よりサイクルを持たないので
を根(root)と呼ぶ。木はその定義よりサイクルを持たないので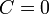 。また平均頂点間距離は、距離L以内にある頂点を数えることで求められる。
。また平均頂点間距離は、距離L以内にある頂点を数えることで求められる。
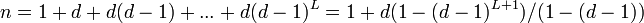 ∝
∝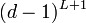
すなわち
Erdős–Rényiグラフ
全ての頂点間に一定の確率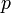 で独立に辺を作成してできるランダムグラフをErdős–Rényiグラフと呼ぶ。各頂点に注目してみると
で独立に辺を作成してできるランダムグラフをErdős–Rényiグラフと呼ぶ。各頂点に注目してみると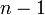 点に対して確率
点に対して確率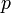 で辺を張るため、次数は二項分布
で辺を張るため、次数は二項分布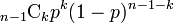 に従う。すなわち次数の平均は
に従う。すなわち次数の平均は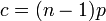 と書ける。
と書ける。
ネットワークの進化
次数の平均値 を変化させて生じるグラフ形状の違いを検証しよう。
を変化させて生じるグラフ形状の違いを検証しよう。
辺の生成される確率が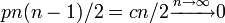 になるため、辺を持たない。
になるため、辺を持たない。
辺があったとしても木にしかならない。
各頂点が定数本の辺を持ちはじめる。ちょうど1本だけだと二部グラフのマッチング、2本だと閉路の集合になる。各頂点が持つ辺の本数(の期待値)が なので、
なので、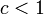 のとき連結しても大きさは高々
のとき連結しても大きさは高々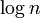 程度にしかならない。しかし
程度にしかならない。しかし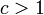 の場合繋がっていく確率のほうが高く、その半径(diameter)を
の場合繋がっていく確率のほうが高く、その半径(diameter)を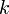 とおくと
とおくと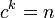 まで成長する。このとき
まで成長する。このとき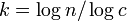 。臨界点にあたる
。臨界点にあたる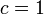 では連結した頂点のサイズが
では連結した頂点のサイズが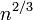 になることが知られている。
になることが知られている。
全体が連結になる。ある頂点が辺を全く持たない確率は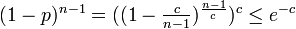 。したがって、そのような頂点がグラフ中に存在しない確率の上限は
。したがって、そのような頂点がグラフ中に存在しない確率の上限は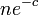 となり、これを0に収束させるには例えば
となり、これを0に収束させるには例えば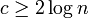 で十分である。つまり、孤立点が消滅する。
で十分である。つまり、孤立点が消滅する。
ネットワークの特徴
- クラスター係数
- 辺が張られる確率は全て独立なので
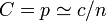 。これは
。これは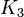 や
や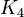 をあまり含まないことを意味している。
をあまり含まないことを意味している。
- 平均頂点間距離
- 各頂点が持つ辺の期待値を
 として半径
として半径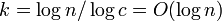 。
。
- 連結性
- Erdős–Rényiグラフ全体が連結であるためには次数が
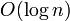 以上必要。
以上必要。