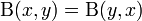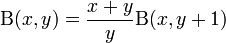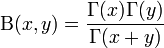Aritalab:Lecture/Math/Function
From Metabolomics.JP
< Aritalab:Lecture | Math(Difference between revisions)
m (→ガンマ関数) |
(→ベータ関数) |
||
| (One intermediate revision by one user not shown) | |||
| Line 14: | Line 14: | ||
:<math>\Gamma(z+1/2) = \frac{(2n)!}{2^{2n}n!}\sqrt{\pi}</math> | :<math>\Gamma(z+1/2) = \frac{(2n)!}{2^{2n}n!}\sqrt{\pi}</math> | ||
| − | ;Stirling | + | ;Stirling の近似 |
| − | :<math>\Gamma(z+1) = z! \sim \sqrt{2\pi z} (\frac{z}{e})^z </math> | + | :<math>\Gamma(z+1) = z! \sim \sqrt{2\pi z} \Big(\frac{z}{e}\Big)^z </math> |
==ベータ関数== | ==ベータ関数== | ||
| Line 26: | Line 26: | ||
:<math>\Beta(x,y) = \frac{x+y}{y} \Beta(x,y+1)\,</math> | :<math>\Beta(x,y) = \frac{x+y}{y} \Beta(x,y+1)\,</math> | ||
:<math>\Beta(x,y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x + y)}</math> | :<math>\Beta(x,y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x + y)}</math> | ||
| − | :<math>\Beta(\frac{1}{2},\frac{1}{2}) = \pi\,</math> | + | :<math>\textstyle \Beta(\frac{1}{2},\frac{1}{2}) = \pi\,</math> |
Latest revision as of 21:26, 20 July 2011
[edit] ガンマ関数
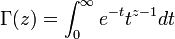
は階乗の一般化で 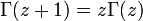 を満たす。z が正の整数の場合は
を満たす。z が正の整数の場合は
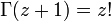
- 例
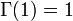
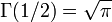
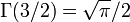
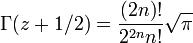
- Stirling の近似
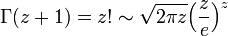
[edit] ベータ関数
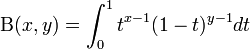
- 例