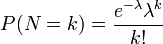Aritalab:Lecture/JSBi/Test/Math
From Metabolomics.JP
< Aritalab:Lecture | JSBi/Test(Difference between revisions)
(→正規分布表) |
|||
| Line 22: | Line 22: | ||
:<math>Corr[X,Y] = Cov[X,Y] /(V[X]^{1/2}V[Y]^{1/2})</math> | :<math>Corr[X,Y] = Cov[X,Y] /(V[X]^{1/2}V[Y]^{1/2})</math> | ||
| − | ==正規分布表== | + | ==分布== |
| + | |||
| + | ==正規分布== | ||
| + | よく見る釣鐘型の分布。どんな分布でも、その中から要素をランダムに抽出して和をとったものの分布は、正規分布に近づく（中心極限定理）。期待値が0, 分散が1になるようにスケーリングしたものを標準正規分布といい、<math>N(0,1)</math>と書く。 | ||
| + | |||
| + | ===正規分布表=== | ||
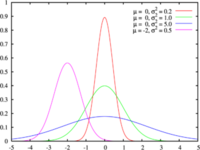
標準正規分布表の見方。 | 標準正規分布表の見方。 | ||
{| | {| | ||
| Line 37: | Line 42: | ||
| 3.0 || 0.0013 || 0.0007 || 0.0003 || 0.0002 || 0.0001 | | 3.0 || 0.0013 || 0.0007 || 0.0003 || 0.0002 || 0.0001 | ||
|} | |} | ||
| − | | [[Image:JSBi- | + | | [[Image:JSBi-Std.png|200px]] |
|} | |} | ||
表におけるzの値は上から順に左→右方向にみる。正規分布全体の面積を1.0としたときの、 | 表におけるzの値は上から順に左→右方向にみる。正規分布全体の面積を1.0としたときの、 | ||
zから上側の面積を示している。例えば標準偏差が2.0以上の面積は0.0228、2.2以上の面積は0.0139。 | zから上側の面積を示している。例えば標準偏差が2.0以上の面積は0.0228、2.2以上の面積は0.0139。 | ||
| + | |||
| + | ==ポアソン分布== | ||
| + | 稀にしか起こらない離散的な事象を数える際に用いる分布。 | ||
| + | 単位時間中に平均λ回発生する事象が、ぴったりk回発生する確率を | ||
| + | :<math>P(N=k) = \frac{e^{-\lambda}\lambda^k}{k!}</math> | ||
| + | と定義する。 | ||
Revision as of 16:53, 8 October 2010
Contents |
確率・統計
平均
期待値とは、確率変数の取る値とその確率とをかけた総和である。フェアなサイコロのように全ての目が糖確率で出る場合は、目の数の期待値は（算術）平均に等しくなる。二つの確率変数X,Yがあったとき、和の平均は平均の和に等しい。
![E[X+Y]=E[X]+E[Y]](/mediawiki/images/math/b/2/8/b2878846b9242595fd3b6b27bb32c83b.png)
X,Yが独立のときに限り、積についても分配できる。
![E[XY]=E[X]E[Y]](/mediawiki/images/math/2/4/e/24e57b4c4766bb198576936fa4dd6e7e.png)
（ただしX,Yは独立）
分散
分散とは確率変数がとる値のばらつきの度合いである。
![V[X] = E[(X-E[X])^2] = E[X^2] - (E[X])^2](/mediawiki/images/math/a/8/5/a85588f23cbb363197b6e033c8d3edd4.png)
X,Yが独立のときに限り、和の分散は分散の和に等しい。
![V[X+Y] = V[X] + V[Y]](/mediawiki/images/math/4/2/3/4230cd5208e2663855b06c131d806da2.png)
（ただしX,Yは独立）
独立でない場合に生じる「ズレ」を共分散と呼ぶ。
![V[X+Y] = V[X] + V[Y] + 2Cov[X,Y]](/mediawiki/images/math/a/b/c/abc1a436af9d1ce47241d60c28236ec0.png)
共分散・相関
共分散は二組の対応する確率変数の間で、ばらつきが異なる度合いである。 共分散の定義は
![Cov[X,Y]=E[ (X-E[X]) (Y-E[Y]) ]](/mediawiki/images/math/4/9/3/4933b69a9fb47270a6166b98c8a5ac30.png)
となる。 XとYに関して対称に定義されていて、XとYのばらつきの傾向が似ていれば大きな正の値になり、似ていなければ大きな負の値になる。XとYが独立であれば0になる。 共分散をXの標準偏差とYの標準偏差で割ったものが相関係数である。
![Corr[X,Y] = Cov[X,Y] /(V[X]^{1/2}V[Y]^{1/2})](/mediawiki/images/math/5/c/d/5cdc472a0bd4515066b5be5877a20647.png)
分布
正規分布
よく見る釣鐘型の分布。どんな分布でも、その中から要素をランダムに抽出して和をとったものの分布は、正規分布に近づく（中心極限定理）。期待値が0, 分散が1になるようにスケーリングしたものを標準正規分布といい、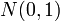
と書く。
正規分布表
標準正規分布表の見方。
|
|
表におけるzの値は上から順に左→右方向にみる。正規分布全体の面積を1.0としたときの、 zから上側の面積を示している。例えば標準偏差が2.0以上の面積は0.0228、2.2以上の面積は0.0139。
ポアソン分布
稀にしか起こらない離散的な事象を数える際に用いる分布。 単位時間中に平均λ回発生する事象が、ぴったりk回発生する確率を
と定義する。
