Aritalab:Lecture/Bioinformatics/Protein

From Metabolomics.JP
< Aritalab:Lecture | Bioinformatics(Difference between revisions)
Jump to: navigation, search
m (→‎スレッディング)
m
 
Line 1: Line 1:
−
===構造比較の尺度 RMSD===
+
==構造比較の尺度 RMSD==
 +
 
 
RMSD (root mean square deviation) は二つの点集合  
 
RMSD (root mean square deviation) は二つの点集合  
 
<math>X = { x_1, x_2, \cdots, x_N} </math> と
 
<math>X = { x_1, x_2, \cdots, x_N} </math> と
Line 10: Line 11:
 
例えば PDB に登録されている二つのタンパク質の構造類似度を測るには、ポリペプチドのC<sub>&alpha;</sub> 座標群を回転・平行移動させてできるだけ重ね合わせたときの RMSD を用います。
 
例えば PDB に登録されている二つのタンパク質の構造類似度を測るには、ポリペプチドのC<sub>&alpha;</sub> 座標群を回転・平行移動させてできるだけ重ね合わせたときの RMSD を用います。
  
−
===Ab Initio構造予測===
+
==Ab Initio構造予測==
  
 
どのフォルドを取るかあらかじめ決めずに配列から構造を予測します。
 
どのフォルドを取るかあらかじめ決めずに配列から構造を予測します。
Line 17: Line 18:
 
* フラグメントアセンブリ ... 9残基など決められたウィンドウ毎に既知構造ライブラリの中から形状を切り出し、ランダムに入れ替えながら構造を最適化します。（ランダムに入れ替えるのでモンテカルロ法の一種です。） 200残基以下のタンパク質であれば、構造を大体予測できるようになってきました。
 
* フラグメントアセンブリ ... 9残基など決められたウィンドウ毎に既知構造ライブラリの中から形状を切り出し、ランダムに入れ替えながら構造を最適化します。（ランダムに入れ替えるのでモンテカルロ法の一種です。） 200残基以下のタンパク質であれば、構造を大体予測できるようになってきました。
  
−
===分子の力場===
+
====分子の力場====
  
 
タンパク質は巨大なため、構造を量子力学の立場で記述するとあまりに複雑です。
 
タンパク質は巨大なため、構造を量子力学の立場で記述するとあまりに複雑です。
Line 23: Line 24:
 
代表的な分子力場のモデルには CHARMM (Chemistry at Harvard using Molecular Mechanics) や AMBER (Assisted Model Building with Energy Refinement) があります。
 
代表的な分子力場のモデルには CHARMM (Chemistry at Harvard using Molecular Mechanics) や AMBER (Assisted Model Building with Energy Refinement) があります。
  
−
まず分子全体のエネルギーを以下のように表します。アミノ酸 ''N'' 個の座標を <math>r^N</math> と表現します。
+
分子全体のエネルギーは例えば以下のように表します。アミノ酸 ''N'' 個の座標を <math>r^N</math> と表現します。
  
 
<math>
 
<math>
Line 46: Line 47:
 
二項目がクーロン力で、全ての C<sub>&alpha;</sub> 間に定義される長距離相互作用になります。電荷 <math> q_i,\ q_j</math> が距離 <math>r_{ij}</math> だけ0離れたときのエネルギーを計算しています。<math>\epsilon_0</math> は真空の誘電率です。　最後の項は、ファンデルワールス相互作用で、 Lennard-Jones の12-6ポテンシャルという概念に従うと考えます。
 
二項目がクーロン力で、全ての C<sub>&alpha;</sub> 間に定義される長距離相互作用になります。電荷 <math> q_i,\ q_j</math> が距離 <math>r_{ij}</math> だけ0離れたときのエネルギーを計算しています。<math>\epsilon_0</math> は真空の誘電率です。　最後の項は、ファンデルワールス相互作用で、 Lennard-Jones の12-6ポテンシャルという概念に従うと考えます。
  
−
===スレッディング===
+
==スレッディング==
  
 
あらかじめ正解の構造がデータベース中にあると仮定して、類似配列を検索する手法です。
 
あらかじめ正解の構造がデータベース中にあると仮定して、類似配列を検索する手法です。

Latest revision as of 09:25, 21 December 2011

Contents

[edit] 構造比較の尺度 RMSD

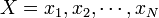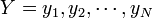RMSD (root mean square deviation) は二つの点集合 X = { x_1, x_2, \cdots, x_N} と Y = { y_1, y_2, \cdots, y_N} (具体的にはタンパク質を構成するポリペプチドのCα座標) の間に定義される距離の平均値という意味で、次の式であらわされます。

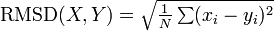
\textstyle \mbox{RMSD}(X,Y) = \sqrt{\frac{1}{N}\sum (x_i - y_i)^{2} }

例えば PDB に登録されている二つのタンパク質の構造類似度を測るには、ポリペプチドのCα 座標群を回転・平行移動させてできるだけ重ね合わせたときの RMSD を用います。

[edit] Ab Initio構造予測

どのフォルドを取るかあらかじめ決めずに配列から構造を予測します。

  • 分子力学 ... エネルギーが低くなる方向に原子を移動して最適化
  • 分子動力学 ... 原子をニュートンの運動方程式に従って動かして最適化
  • フラグメントアセンブリ ... 9残基など決められたウィンドウ毎に既知構造ライブラリの中から形状を切り出し、ランダムに入れ替えながら構造を最適化します。（ランダムに入れ替えるのでモンテカルロ法の一種です。） 200残基以下のタンパク質であれば、構造を大体予測できるようになってきました。

[edit] 分子の力場

タンパク質は巨大なため、構造を量子力学の立場で記述するとあまりに複雑です。 そのため Cα 座標のみを用いた力学系で解釈する分子力学がよく使われます。 代表的な分子力場のモデルには CHARMM (Chemistry at Harvard using Molecular Mechanics) や AMBER (Assisted Model Building with Energy Refinement) があります。

分子全体のエネルギーは例えば以下のように表します。アミノ酸 N 個の座標を 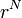r^N と表現します。

\begin{align} V(r^N) &= \textstyle \Big( \sum_{i} \frac{k_i}{2} (l_i - l_{i0})^2 + \sum_{j} \frac{k_j}{2} (\theta_j - \theta_{j0})^2 + \sum \frac{V_n}{2} ( 1 + \cos (n\omega - \gamma) ) \Big)\\ &+ \textstyle\sum_{i=1}^N \sum_{j=i+1}^N \frac{q_iq_j}{4\pi \epsilon_0 r_{ij}}\\ &+ \textstyle\sum_{i=1}^N \sum_{j=i+1}^N 4 \epsilon_{ij} \Big[ \Big( \frac{\sigma_{ij}}{r_{ij}} \Big)^{12} - \Big( \frac{\sigma_{ij}}{r_{ij}} \Big)^6 \Big] \end{align}

最初の項は共有結合によるエネルギーです。さらに、結合距離、結合角度、結合のねじれに関するエネルギーから構成されます。

  • 結合距離 (bond distance)

原子間の結合に対して定められる基準距離 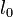l_0 から伸縮して生成するエネルギーはフックの法則に従うと考えます。パラメータは 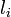l_i です。

  • 原子価角度 (valence angle)

Cα が接続する角度がねじれて生成するエネルギーも、フックの法則（二次式）に従うと考えます。同様に 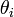\theta_i がパラメータです。

  • ねじれ角

ここにおける 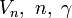V_n, \ n, \ \gamma は原子の種類や配置によって決まる定数で、二面角 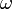\omega がパラメータになります。 ねじれ角のエネルギーは結合距離や原子価角度によるものより小さく、二面角は立体構造の中で柔軟に動きうる部分です。

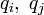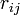二項目がクーロン力で、全ての Cα 間に定義される長距離相互作用になります。電荷 q_i,\ q_j が距離 r_{ij} だけ0離れたときのエネルギーを計算しています。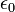\epsilon_0 は真空の誘電率です。　最後の項は、ファンデルワールス相互作用で、 Lennard-Jones の12-6ポテンシャルという概念に従うと考えます。

[edit] スレッディング

あらかじめ正解の構造がデータベース中にあると仮定して、類似配列を検索する手法です。

ホモロジーモデリング
アミノ酸が30%以上保存されるような配列を検索するのに向いています。データベースに登録された鋳型構造にあうようにアミノ酸配列を重ねあわせます。大きなサイズのタンパク質でも対応できます。
3D-1D法、Verify3D
3D-1D法は、タンパク質の立体構造を考える上で20種のアミノ酸を区別する必然性は無いことに注目します。各アミノ酸に環境（極性か非極性か、タンパク質の内側か外側か）分類と二次構造のカテゴリーを割り当て、タンパク質の立体構造と一次構造の整合性を評価する指標を作ります。


[edit] ツール、ソフトウェア

ナショナルバイオデータベースセンターによるツールの紹介は こちら。 タンパク質構造に関しては大変多くのソフトウェアが開発されています。精度は対象によっても大きく異なるので、使いやすいツールを紹介しておきます。

  • アミノ酸配列からの立体構造予測 Swiss Model
  • アミノ酸配列からのドメイン、二次構造予測　InterProScan


参考
Retrieved from "http://metabolomics.jp/mediawiki/index.php?title=Aritalab:Lecture/Bioinformatics/Protein&oldid=254808"
Personal tools
Namespaces

Variants
Actions
Navigation
metabolites
Toolbox