Aritalab:Lecture/Basic/Probability Generating Function
From Metabolomics.JP
< Aritalab:Lecture | Basic(Difference between revisions)
m (→一様分布) |
|||
| Line 51: | Line 51: | ||
</math> | </math> | ||
| − | この式は<math>1-z</math>を分母に含んでしまうため、<math>\mbox{U}_n'(1)</math>や<math>\mbox{U}_n''(1)</math> | + | この式は<math>1-z</math>を分母に含んでしまうため、<math>\mbox{U}_n'(1)</math>や<math>\mbox{U}_n''(1)</math>を求める際に不都合である。そこでテイラーの定理を応用する。 |
<math> | <math> | ||
| Line 81: | Line 81: | ||
\mbox{U}_n''(1) + \mbox{U}_n'(1) - \mbox{U}_n'(1)^2 = \frac{n^2-1}{12}. | \mbox{U}_n''(1) + \mbox{U}_n'(1) - \mbox{U}_n'(1)^2 = \frac{n^2-1}{12}. | ||
</math> | </math> | ||
| − | |||
==ポアソン分布== | ==ポアソン分布== | ||
Revision as of 09:15, 3 June 2010
Contents |
確率母関数
ある確率分布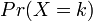 の確率母関数(probability generating function または pgf)を以下のように定義する。
の確率母関数(probability generating function または pgf)を以下のように定義する。
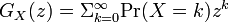
確率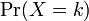 は全て正の値でkについて全て足しあわせると1になる。
は全て正の値でkについて全て足しあわせると1になる。
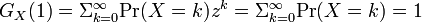
逆に係数が非負で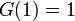 であるようなべき級数
であるようなべき級数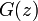 があれば、それは何らかの確率母関数である。
があれば、それは何らかの確率母関数である。
平均と分散
確率母関数を使うと平均と分散の計算が容易にできる。
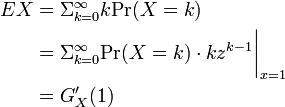
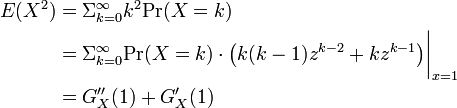
したがって
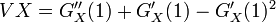
一様分布
n次の一様分布(uniform distribution)とは確率変数が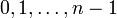 の値を確率
の値を確率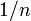 でとるもの。
でとるもの。
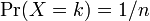
確率母関数は以下の等比級数になる。
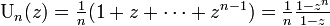
この式は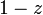 を分母に含んでしまうため、
を分母に含んでしまうため、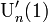 や
や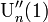 を求める際に不都合である。そこでテイラーの定理を応用する。
を求める際に不都合である。そこでテイラーの定理を応用する。
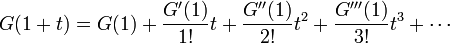
この係数、つまり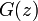 の導関数を以下の式と見比べればよい。
の導関数を以下の式と見比べればよい。
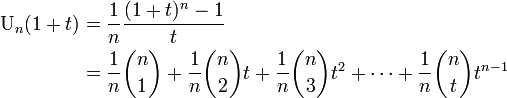
ここから
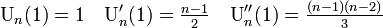
平均と分散は
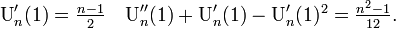
ポアソン分布
ポアソン分布とは単位時間中に平均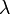 回発生する事象がちょうどk回発生する確率。
回発生する事象がちょうどk回発生する確率。
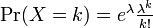
確率母関数は
Failed to parse (lexing error): \textstyle \begin{align} G(z) &= \Sigma_{k=0}^{\infty} e^{\lambda}\frac{\lambda^k}{k!} z^k = e^{\lambda}\Sigma_{k=0}^{\infty}\frac{(\lambda z)^k}{k!} = e^{\lambda} e^{\lambda z} \\ &= e^{\lambda (z-1)} \end{align}
平均と分散は