Aritalab:Lecture/NetworkBiology/Percolation on Graph
From Metabolomics.JP
< Aritalab:Lecture | NetworkBiology(Difference between revisions)
m |
m |
||
| (24 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | + | {{Lecture/Header}} | |
| − | + | ==グラフ上のパーコレーション== | |
| − | + | ||
| + | グラフをある次数分布に従うツリーとみなすことで、パーコレーションを扱ってみます。ここでの議論は[[Aritalab:Lecture/Basic/GF_DegreeDistribution|母関数を使った説明]]もあります。 | ||
| − | + | あるネットワークの平均次数が <k> で与えられるとき、隣接点の平均次数は <math>\textstyle \frac{\langle k^2 \rangle - \langle k \rangle}{\langle k \rangle}</math> になります。この本数のうち、確率 q でサイトが ON になる場合、隣接点の周りで占有される頂点数は <math>q \textstyle \frac{\langle k^2 \rangle - \langle k \rangle}{\langle k \rangle}</math> になります。これが 1 を上回る場合に相転移をおこすので、臨界確率 <math>q_c = \textstyle \frac{1}{\langle k^2 \rangle / \langle k \rangle - 1 }</math> が得られます。つまり、<k<sup>2</sup>> / <k> のバランスに臨界確率が左右されるということです。 | |
| − | + | ||
| − | + | ==パーコレーションの起こりやすさ== | |
| + | いかなる次数分布でも、<math>\langle k^2 \rangle</math>が<math>\langle k \rangle</math>に比して大きいと、低い浸透確率で相転移が起こります。 | ||
| − | + | ===格子グラフ、Erdosブラフ=== | |
| + | 次数が一定の場合、<math>\langle k^2 \rangle = \langle k \rangle^2</math> です。すなわち、<math>q_c = 1 / \langle k \rangle</math> となります。 | ||
| + | |||
| + | 次数分布がポアソン分布をなす場合、平均と分散は等しく <math>E[k] = V[k] = \langle k \rangle </math> になります。 | ||
| + | このとき <math>\langle k^2 \rangle = \langle k \rangle^2 + \langle k \rangle </math> です。この場合も格子グラフとほぼ同じで、平均次数に反比例して浸透確率が下がります。 | ||
| + | |||
| + | ===スケールフリーネットワーク=== | ||
| + | |||
| + | 次数の分布が、べき分布 <math>p(k)=Ck^{-\gamma}</math> のときをかんがえましょう。 | ||
| + | ここで <math>\zeta(\gamma)\ </math> はリーマンゼータ関数とします。 | ||
| + | |||
| + | <math> | ||
| + | \frac{\langle k^2 \rangle}{\langle k \rangle} = \frac{\Sigma_kk^2p(k)}{\Sigma_kkp(k)} = \frac{\Sigma k^{2-\gamma}}{ \Sigma k^{1-\gamma}} = \frac{\zeta(\gamma - 2)}{\zeta(\gamma - 1)} | ||
| + | </math> | ||
| + | |||
| + | この値は<math>\gamma \leq 3</math>のときに発散します。また <math>\gamma</math> が大きくなると <math> k=1 </math> の項が大きな要素を占めるのでほとんど 1 に近づきます。 | ||
<!---- | <!---- | ||
| + | |||
| + | 別の書き方では<math>\Sigma k(k-2)p(k) = 0</math>だが、この和のうち負の値になるのは<math>k=1</math>のときだけ、つまり行き止まりが極端に多くない限り、連結成分は繋がって無限に大きくなることを意味している。 | ||
| + | |||
==連結成分のサイズの母関数== | ==連結成分のサイズの母関数== | ||
ランダムに選んだ辺から出発したときの連結成分のサイズの分布を<math>H_e(x)</math>、ランダムに選んだ頂点を含む連結成分のサイズの分布を<math>H_v(x)</math>と書こう。辺を選んだとき、連結成分が先に広がるかどうかはもう片側にある端点の次数に依存し、その分布は<math>\textstyle kp(k)/\Sigma_j jp(j)</math>である。それぞれの先からも辺が伸びていくため | ランダムに選んだ辺から出発したときの連結成分のサイズの分布を<math>H_e(x)</math>、ランダムに選んだ頂点を含む連結成分のサイズの分布を<math>H_v(x)</math>と書こう。辺を選んだとき、連結成分が先に広がるかどうかはもう片側にある端点の次数に依存し、その分布は<math>\textstyle kp(k)/\Sigma_j jp(j)</math>である。それぞれの先からも辺が伸びていくため | ||
| Line 19: | Line 37: | ||
連結成分のサイズの期待値は<math>H_v'(1) = G_v(H_e(1)) + G_v'(1)H_e'(1)=</math> | 連結成分のサイズの期待値は<math>H_v'(1) = G_v(H_e(1)) + G_v'(1)H_e'(1)=</math> | ||
| − | |||
| − | + | ||
パーコレーションにおいては、確率<math>(1-q)</math>で辺が繋がらなくなる。実効的な次数が<math>\bar{k}</math>になる確率は<math>\bar{p}(\bar{k}) = \Sigma_{k=\bar{k}}^{\infty}p(k) \tbinom{k}{\bar{k}}q^{\bar{k}}(1-q)^{k-\bar{k}}</math>である。 | パーコレーションにおいては、確率<math>(1-q)</math>で辺が繋がらなくなる。実効的な次数が<math>\bar{k}</math>になる確率は<math>\bar{p}(\bar{k}) = \Sigma_{k=\bar{k}}^{\infty}p(k) \tbinom{k}{\bar{k}}q^{\bar{k}}(1-q)^{k-\bar{k}}</math>である。 | ||
| − | + | ||
このとき<math>\langle \bar{k} \rangle = \langle k \rangle q</math>、<math>\langle \bar{k^2} \rangle = \langle k^2 \rangle + \langle k \rangle q (1-q)</math>になる。 | このとき<math>\langle \bar{k} \rangle = \langle k \rangle q</math>、<math>\langle \bar{k^2} \rangle = \langle k^2 \rangle + \langle k \rangle q (1-q)</math>になる。 | ||
| − | |||
| − | 大雑把に言うと相転移を起こすのは<math>\langle k^2 \rangle q^2= 2 \langle k \rangle q</math>のとき、つまり<math>q = 2 \langle k \rangle / \langle k^2 \rangle</math>のあたりである。 | + | |
| + | 大雑把に言うと相転移を起こすのは<math>\langle k^2 \rangle q^2= 2 \langle k \rangle q</math>のとき、つまり<math>q = 2 \langle k \rangle / \langle k^2 \rangle</math>のあたりである。 | ||
| + | ----> | ||
Latest revision as of 12:19, 6 August 2016
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
[edit] グラフ上のパーコレーション
グラフをある次数分布に従うツリーとみなすことで、パーコレーションを扱ってみます。ここでの議論は母関数を使った説明もあります。
あるネットワークの平均次数が <k> で与えられるとき、隣接点の平均次数は 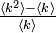 になります。この本数のうち、確率 q でサイトが ON になる場合、隣接点の周りで占有される頂点数は
になります。この本数のうち、確率 q でサイトが ON になる場合、隣接点の周りで占有される頂点数は 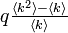 になります。これが 1 を上回る場合に相転移をおこすので、臨界確率
になります。これが 1 を上回る場合に相転移をおこすので、臨界確率 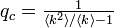 が得られます。つまり、<k2> / <k> のバランスに臨界確率が左右されるということです。
が得られます。つまり、<k2> / <k> のバランスに臨界確率が左右されるということです。
[edit] パーコレーションの起こりやすさ
いかなる次数分布でも、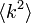 が
が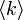 に比して大きいと、低い浸透確率で相転移が起こります。
に比して大きいと、低い浸透確率で相転移が起こります。
[edit] 格子グラフ、Erdosブラフ
次数が一定の場合、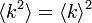 です。すなわち、
です。すなわち、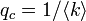 となります。
となります。
次数分布がポアソン分布をなす場合、平均と分散は等しく ![E[k] = V[k] = \langle k \rangle](/mediawiki/images/math/a/0/8/a08c7b8e48d6939e5f49fc09c58327bc.png) になります。
このとき
になります。
このとき 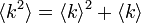 です。この場合も格子グラフとほぼ同じで、平均次数に反比例して浸透確率が下がります。
です。この場合も格子グラフとほぼ同じで、平均次数に反比例して浸透確率が下がります。
[edit] スケールフリーネットワーク
次数の分布が、べき分布 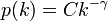 のときをかんがえましょう。
ここで
のときをかんがえましょう。
ここで 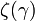 はリーマンゼータ関数とします。
はリーマンゼータ関数とします。
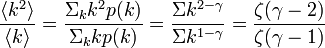
この値は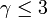 のときに発散します。また
のときに発散します。また 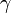 が大きくなると
が大きくなると 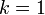 の項が大きな要素を占めるのでほとんど 1 に近づきます。
の項が大きな要素を占めるのでほとんど 1 に近づきます。