Aritalab:Lecture/NetworkBiology/Percolation
m (→木またはベーテ格子の場合) |
m |
||
| Line 10: | Line 10: | ||
{| class="wikitable" style="float:right" | {| class="wikitable" style="float:right" | ||
|- | |- | ||
| − | !colspan=3| 主な浸透閾値<math>p_c</math> (* | + | !colspan=3| 主な浸透閾値<math>p_c</math> (*のみ厳密解。<br/>ほとんどの場合解析的に解けない。) |
|- | |- | ||
! 格子の種類 || サイト || ボンド | ! 格子の種類 || サイト || ボンド | ||
| Line 37: | Line 37: | ||
|} | |} | ||
| − | == | + | ==クラスター・周縁という概念== |
各格子点は確率 ''p'' で占有されるとし、占有された格子点の集まりをクラスターと呼ぶ。特に、大きさが ''s'' のクラスターを ''s-''クラスターと呼ぶ。クラスターの周囲の格子点は空でなくてはならない。クラスターに隣接する空の格子点群を周縁 (perimeter) と呼ぶ。クラスターが大きくなると内部にも周縁が存在しうるので、周縁と周囲は異なることに注意しよう。 | 各格子点は確率 ''p'' で占有されるとし、占有された格子点の集まりをクラスターと呼ぶ。特に、大きさが ''s'' のクラスターを ''s-''クラスターと呼ぶ。クラスターの周囲の格子点は空でなくてはならない。クラスターに隣接する空の格子点群を周縁 (perimeter) と呼ぶ。クラスターが大きくなると内部にも周縁が存在しうるので、周縁と周囲は異なることに注意しよう。 | ||
| − | ある格子点を含む、大きさ ''s'' 、周縁 ''t'' の異なるクラスターの数を <math>a_{s,t}</math> | + | ある格子点を含む、大きさ ''s'' 、周縁 ''t'' の異なるクラスターの数を <math>a_{s,t}</math> であらわす。2次元格子の場合、以下のようになる。占有点を黒、非占有点を白、注目している格子点を灰色であらわしている。 |
| − | <math>a_{1,4} = 1 \quad a_{2,6} = 4 \quad a_{3, | + | <math>a_{1,4} = 1 \quad a_{2,6} = 4 \quad a_{3,8} = 6 \quad a_{3,7} = 12 </math> |
| + | |||
| + | [[File:Lecture-NetworkBiology-Percolation.png]] | ||
==母関数とよく使う記法== | ==母関数とよく使う記法== | ||
これからよく使う記法を[[Aritalab:Lecture/Basic/Generating_Function|母関数]] <math>\textstyle A(x,y) = \sum_{s,t} a_{s,t} x^s y^t</math> を使ってまとめておく。 | これからよく使う記法を[[Aritalab:Lecture/Basic/Generating_Function|母関数]] <math>\textstyle A(x,y) = \sum_{s,t} a_{s,t} x^s y^t</math> を使ってまとめておく。 | ||
| − | * ある格子点が、大きさ''s''、周縁''t''のクラスターに含まれる確率 | + | * ある格子点が、大きさ ''s''、周縁 ''t'' のクラスターに含まれる確率 |
:<math>\textstyle p_{s,t} = a_{s,t} p^s (1-p)^t</math> | :<math>\textstyle p_{s,t} = a_{s,t} p^s (1-p)^t</math> | ||
* ある格子点が、''s''-クラスターに含まれる確率 | * ある格子点が、''s''-クラスターに含まれる確率 | ||
:<math>\textstyle P_s = \sum_t p_{s,t}</math> | :<math>\textstyle P_s = \sum_t p_{s,t}</math> | ||
| − | * ある格子点が、有限の大きさのクラスターに含まれる確率 | + | * ある格子点が、有限の大きさのクラスターに含まれる確率 (''s'', ''t'' に関する和は有限個) |
:<math>\textstyle F = \sum_{s,t} p_{s,t} = \sum_s P_s = A(p, 1-p)</math> | :<math>\textstyle F = \sum_{s,t} p_{s,t} = \sum_s P_s = A(p, 1-p)</math> | ||
| − | * ある格子点が、無限大のクラスターに含まれる確率 (= | + | * ある格子点が、無限大のクラスターに含まれる確率 (=浸透確率と呼ぶ) |
:<math>\textstyle P_{\infty} = p - F</math> | :<math>\textstyle P_{\infty} = p - F</math> | ||
* ある格子点が含まれる、有限の大きさのクラスターの平均サイズ | * ある格子点が含まれる、有限の大きさのクラスターの平均サイズ | ||
:<math>S = \frac{\sum_{s,t} s p_{s,t}}{F} = \frac{\sum_s s P_s}{\sum_s P_s} = x\frac{\partial}{\partial x}\log A(x,y) \Bigg|_{x=p,\ y=1-p}</math> | :<math>S = \frac{\sum_{s,t} s p_{s,t}}{F} = \frac{\sum_s s P_s}{\sum_s P_s} = x\frac{\partial}{\partial x}\log A(x,y) \Bigg|_{x=p,\ y=1-p}</math> | ||
| − | + | ||
| − | + | これらを使って、浸透確率 (ある格子点が、無限大のクラスターに含まれる確率)と、クラスターの平均サイズを調べよう。 | |
==一次元の場合== | ==一次元の場合== | ||
一次元の場合は、無限に長い直線上に、定められた間隔で格子点をおく。 | 一次元の場合は、無限に長い直線上に、定められた間隔で格子点をおく。 | ||
| − | + | 無限に伸びるクラスターができるためには全ての格子点が占有されなくてはならないので、浸透閾値 <math>p_c=1</math> である。 | |
| − | また、周縁サイズは常に<math>t=2</math>の1パターンのみとなる。 | + | また、周縁サイズは常に <math>t=2</math> の1パターンのみとなる。 |
この簡便さから、多くの問いに対して厳密解を求めることができる。 | この簡便さから、多くの問いに対して厳密解を求めることができる。 | ||
| − | : 母関数 <math>\textstyle A(x,y) = \sum_s s x^s y^2 = \frac{xy^2}{(1-x)^2}</math> | + | : 母関数 <math>\textstyle A(x,y) = \sum_s s x^s y^2 = \frac{xy^2}{(1-x)^2}</math> |
| + | |||
* ある格子点が、''s''-クラスターに含まれる確率 | * ある格子点が、''s''-クラスターに含まれる確率 | ||
:<math>\textstyle P_s = s p_{s,t} = s p^s (1-p)^2</math> | :<math>\textstyle P_s = s p_{s,t} = s p^s (1-p)^2</math> | ||
| − | * | + | |
| + | {| | ||
| + | |valign="top"| | ||
| + | ;<math>p < p_c = 1</math> の場合 | ||
| + | * 浸透確率 | ||
| + | : クラスターは必ず有限なので 0 になる。 | ||
:<math>\textstyle F = \sum_{s,t} p_{s,t} = \sum_s P_s = p</math> | :<math>\textstyle F = \sum_{s,t} p_{s,t} = \sum_s P_s = p</math> | ||
| − | |||
:<math>\textstyle P_{\infty} = p - F = 0</math> | :<math>\textstyle P_{\infty} = p - F = 0</math> | ||
| − | * | + | * クラスターの平均サイズ |
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| − | S &= \textstyle \frac{\sum_{s,t} s p_{s,t}}{F} = \frac{\sum_s s P_s}{\sum_s P_s} | + | S &= \textstyle \frac{\sum_{s,t} s p_{s,t}}{F} = \frac{\sum_s s P_s}{\sum_s P_s} \\ |
| − | = \frac{x}{p} \frac{\partial}{\partial x} A(x,y) \Big|_{x=p,\ y=1-p}\\ | + | &= \frac{x}{p} \frac{\partial}{\partial x} A(x,y) \Big|_{x=p,\ y=1-p}\\ |
&= \textstyle \frac{(1-p)^4 + 2p(1-p)^2(1-p)}{(1-p)^4} = \frac{1+p}{1-p} | &= \textstyle \frac{(1-p)^4 + 2p(1-p)^2(1-p)}{(1-p)^4} = \frac{1+p}{1-p} | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | + | |valign="top"| | |
| − | + | ;<math>p = p_c = 1</math> の場合 | |
| + | * 浸透確率 | ||
| + | : 1 | ||
| + | * クラスターの平均サイズ | ||
| + | : 0 | ||
| + | |} | ||
===相関関数と相関距離=== | ===相関関数と相関距離=== | ||
| Line 99: | Line 111: | ||
==木またはベーテ格子の場合== | ==木またはベーテ格子の場合== | ||
| − | + | 次数が一定で無限に大きな木を、ベーテ格子と呼ぶ(有限の場合はケーリー木と呼んでもよい)。 | |
磁性を扱う方法の一つであるベーテ近似によりこの木の厳密解が求まるため、ベーテ格子と呼ぶようになった。 | 磁性を扱う方法の一つであるベーテ近似によりこの木の厳密解が求まるため、ベーテ格子と呼ぶようになった。 | ||
| − | + | ベーテ格子はサイクルを持たない一次元の場合は、次数が2のベーテ格子と考えられる。 | |
次数が ''d'' の木の場合、原点は ''d'' 本の枝を持つ。 | 次数が ''d'' の木の場合、原点は ''d'' 本の枝を持つ。 | ||
残りの点は通ってきた点のほかに ''d'' − 1 本の枝を持ち、それらの先に確率 ''p'' で占有される格子点が存在する。 | 残りの点は通ってきた点のほかに ''d'' − 1 本の枝を持ち、それらの先に確率 ''p'' で占有される格子点が存在する。 | ||
先に進める確率は (''d'' − 1) ''p'' になるので、無限大のクラスターが存在し始める値は <math>\textstyle p_c=\frac{1}{d-1}</math>。 | 先に進める確率は (''d'' − 1) ''p'' になるので、無限大のクラスターが存在し始める値は <math>\textstyle p_c=\frac{1}{d-1}</math>。 | ||
| − | + | つまり各点に平均 <math>\textstyle \frac{d}{d-1}</math> 本の枝があれば、無限に大きなクラスターが存在する。 | |
逆に、これより低い ''p'' の値では、無限に大きなクラスターは存在しない。 | 逆に、これより低い ''p'' の値では、無限に大きなクラスターは存在しない。 | ||
以降、簡単のため <math>d=3</math>, <math>(p_c = 1/2)</math> に話を限定する。 | 以降、簡単のため <math>d=3</math>, <math>(p_c = 1/2)</math> に話を限定する。 | ||
| Line 133: | Line 145: | ||
! || <math>p < 1/2</math> || <math>p > 1/2</math> | ! || <math>p < 1/2</math> || <math>p > 1/2</math> | ||
|- | |- | ||
| − | | | + | | 有限のクラスターに含まれる確率 ''F'' || ''p'' || <math>(1-p)^3/p^2</math> |
|- | |- | ||
| − | | | + | | 浸透確率 ''P''<sub>∞</sub> = ''p'' − ''F'' || 0 || <math>p - (1-p)^3/p^2</math> |
|} | |} | ||
| Line 148: | Line 160: | ||
次数 ''d'' の場合 <math>p < p_c = 1/(d-1)</math> なら <math>S = (1+p)/(1-dp)</math>。 | 次数 ''d'' の場合 <math>p < p_c = 1/(d-1)</math> なら <math>S = (1+p)/(1-dp)</math>。 | ||
| − | + | まとめると | |
| + | {| class ="wikitable" style="text-align:center" | ||
| + | ! || <math>p < 1/2</math> | ||
| + | |- | ||
| + | | 平均サイズ || <math>(1+p)/(1-2p)</math> | ||
| + | |} | ||
;参考 | ;参考 | ||
<references/> | <references/> | ||
Revision as of 10:11, 10 June 2011
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
パーコレーションとは
パーコレーション(浸透)理論 (percolation theory) では、非常に大きな格子において各格子点が周囲とは全く独立に確率pで占有されるときに生成されるクラスターを解析する。
様々な格子において、確率 p がある閾値 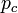 に達すると、無限に大きなクラスターが存在し始める(臨界現象)。この値を浸透閾値 (percolation threshold) と呼ぶ。浸透閾値
に達すると、無限に大きなクラスターが存在し始める(臨界現象)。この値を浸透閾値 (percolation threshold) と呼ぶ。浸透閾値 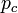 はほとんどの場合について厳密解が求まっていないが、数値シミュレーション等で解析されている。
はほとんどの場合について厳密解が求まっていないが、数値シミュレーション等で解析されている。
上記のように格子点が確率 p で占有される過程を、正確にはサイト過程と呼ぶ。これに対して、格子点と格子点を結ぶ辺(ボンド)が確率 p で開閉されると考えて生成するクラスターを解析する場合を、ボンド過程と呼ぶ。
主な浸透閾値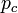 (*のみ厳密解。 (*のみ厳密解。ほとんどの場合解析的に解けない。) | ||
|---|---|---|
| 格子の種類 | サイト | ボンド |
| 蜂の巣 | 0.697043 | 0.65271* |
| 正方 | 0.5927462 | 1/2 * |
| 三角 | 1/2 * | 0.34729* |
| ダイヤモンド | 0.4301 | 0.3893 |
| 単純立方 | 0.311608 | 0.248813 |
| 体心立方 | 0.245691 | 0.180287 |
| 面心立方[1] | 0.199236 | 0.120163 |
| d=4 超立方 | 0.196885 | 0.160131 |
| d=5 超立方 | 0.140797 | 0.118172 |
| d=6 超立方 | 0.109018 | 0.094202 |
| d=7 超立方 | 0.088951 | 0.078675 |
クラスター・周縁という概念
各格子点は確率 p で占有されるとし、占有された格子点の集まりをクラスターと呼ぶ。特に、大きさが s のクラスターを s-クラスターと呼ぶ。クラスターの周囲の格子点は空でなくてはならない。クラスターに隣接する空の格子点群を周縁 (perimeter) と呼ぶ。クラスターが大きくなると内部にも周縁が存在しうるので、周縁と周囲は異なることに注意しよう。
ある格子点を含む、大きさ s 、周縁 t の異なるクラスターの数を 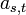 であらわす。2次元格子の場合、以下のようになる。占有点を黒、非占有点を白、注目している格子点を灰色であらわしている。
であらわす。2次元格子の場合、以下のようになる。占有点を黒、非占有点を白、注目している格子点を灰色であらわしている。
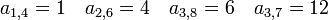
母関数とよく使う記法
これからよく使う記法を母関数 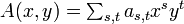 を使ってまとめておく。
を使ってまとめておく。
- ある格子点が、大きさ s、周縁 t のクラスターに含まれる確率
- ある格子点が、s-クラスターに含まれる確率
- ある格子点が、有限の大きさのクラスターに含まれる確率 (s, t に関する和は有限個)
- ある格子点が、無限大のクラスターに含まれる確率 (=浸透確率と呼ぶ)
- ある格子点が含まれる、有限の大きさのクラスターの平均サイズ
これらを使って、浸透確率 (ある格子点が、無限大のクラスターに含まれる確率)と、クラスターの平均サイズを調べよう。
一次元の場合
一次元の場合は、無限に長い直線上に、定められた間隔で格子点をおく。
無限に伸びるクラスターができるためには全ての格子点が占有されなくてはならないので、浸透閾値 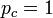 である。
また、周縁サイズは常に
である。
また、周縁サイズは常に 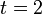 の1パターンのみとなる。
この簡便さから、多くの問いに対して厳密解を求めることができる。
の1パターンのみとなる。
この簡便さから、多くの問いに対して厳密解を求めることができる。
- 母関数
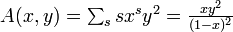
- ある格子点が、s-クラスターに含まれる確率
|
|
相関関数と相関距離
ある占有された格子点から  だけ離れた格子点が同じクラスターに属する確率を
だけ離れた格子点が同じクラスターに属する確率を 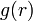 であらわし、相関関数とよぶ。
であらわし、相関関数とよぶ。
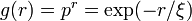
ここで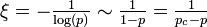 。この
。この 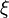 を相関距離という。
を相関距離という。
大まかにいうと、相関距離はクラスターの差し渡しに比例する。 占有確率 p が大きくなると 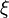 も増え、p が小さくなると
も増え、p が小さくなると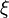 も減る。一次元の場合、 1列に並ぶだけなので
も減る。一次元の場合、 1列に並ぶだけなので 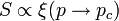 が成立、つまり相関距離はクラスターの平均サイズに比例する。
さらに
が成立、つまり相関距離はクラスターの平均サイズに比例する。
さらに  も成立する。
も成立する。
- 証明
- 一次元の場合、r ステップ離れた箇所まで全ての点が占有されねばならないから
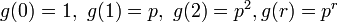 が成立。
が成立。
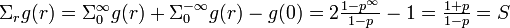 。(証明終)
。(証明終)
木またはベーテ格子の場合
次数が一定で無限に大きな木を、ベーテ格子と呼ぶ(有限の場合はケーリー木と呼んでもよい)。 磁性を扱う方法の一つであるベーテ近似によりこの木の厳密解が求まるため、ベーテ格子と呼ぶようになった。 ベーテ格子はサイクルを持たない一次元の場合は、次数が2のベーテ格子と考えられる。
次数が d の木の場合、原点は d 本の枝を持つ。
残りの点は通ってきた点のほかに d − 1 本の枝を持ち、それらの先に確率 p で占有される格子点が存在する。
先に進める確率は (d − 1) p になるので、無限大のクラスターが存在し始める値は 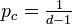 。
つまり各点に平均
。
つまり各点に平均 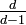 本の枝があれば、無限に大きなクラスターが存在する。
逆に、これより低い p の値では、無限に大きなクラスターは存在しない。
以降、簡単のため
本の枝があれば、無限に大きなクラスターが存在する。
逆に、これより低い p の値では、無限に大きなクラスターは存在しない。
以降、簡単のため 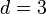 ,
, 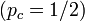 に話を限定する。
母関数を求めるのはややこしいが、興味のある人は「パーコレーションの科学」(小田垣 孝著 裳華房)を参照してほしい。
に話を限定する。
母関数を求めるのはややこしいが、興味のある人は「パーコレーションの科学」(小田垣 孝著 裳華房)を参照してほしい。
d = 3 の木
ここまでの議論から、浸透閾値は 1/2 である。確率が 1/2 を超えると、その頂点にたどり着いた枝を除いた残り 2 本のうちどちらかがつながっているから、無限大のクラスターが存在する。
浸透確率 P∞
ある格子点が、無限大のクラスターに含まれる確率 (=浸透確率)を求めよう。
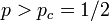 のとき(無限に大きいクラスターがあるとき)、任意の格子点が、それから始まる枝のうち一つを通しては無限遠につながらない確率をQとする。
ある近接した格子点から外に無限遠へつながらない確率は、その格子点が占有されていないか、占有されてもその先でつながらない確率を足したもの。
これはQに等しいはずなので
のとき(無限に大きいクラスターがあるとき)、任意の格子点が、それから始まる枝のうち一つを通しては無限遠につながらない確率をQとする。
ある近接した格子点から外に無限遠へつながらない確率は、その格子点が占有されていないか、占有されてもその先でつながらない確率を足したもの。
これはQに等しいはずなので
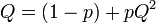
が成立する。これを解くと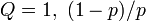 。
。
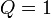 の場合は無限遠に決してつながらず、
の場合は無限遠に決してつながらず、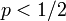 のときの
のときの 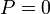 に対応する。
に対応する。
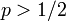 のとき、
のとき、 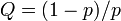 を考える。
原点が占有されていても無限遠につながらない確率は
を考える。
原点が占有されていても無限遠につながらない確率は 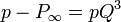 。
これより
。
これより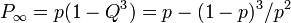 。
。
まとめると
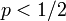 |
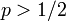
| |
|---|---|---|
| 有限のクラスターに含まれる確率 F | p | 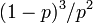
|
| 浸透確率 P∞ = p − F | 0 | 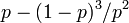
|
クラスターの平均サイズ S
ある枝の先につながっている格子点数の期待値を 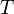 と書く。
まず
と書く。
まず 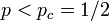 の場合を考える。
どの格子点もサイズが無限大のクラスターには属さない。
従って、枝の先にある格子点が占有されていればその格子点プラス二つの枝の平均サイズが付け加わるから
の場合を考える。
どの格子点もサイズが無限大のクラスターには属さない。
従って、枝の先にある格子点が占有されていればその格子点プラス二つの枝の平均サイズが付け加わるから 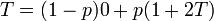 。
これを解くと
。
これを解くと 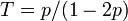 。
従って、ある頂点が属するクラスターの平均サイズは
。
従って、ある頂点が属するクラスターの平均サイズは 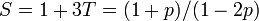 。
この議論は容易に一般化できる。
次数 d の場合
。
この議論は容易に一般化できる。
次数 d の場合 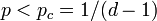 なら
なら 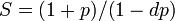 。
。
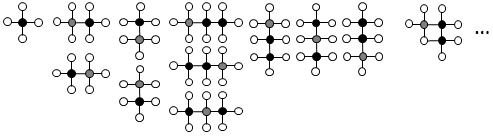
まとめると
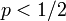
| |
|---|---|
| 平均サイズ | 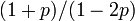
|
- 参考
- ↑ 同半径の球を敷き詰めたときの最密充填
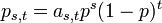
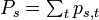
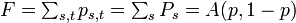
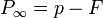
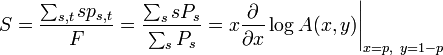
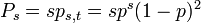
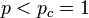 の場合
の場合
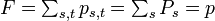
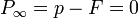
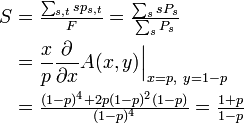
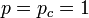 の場合
の場合