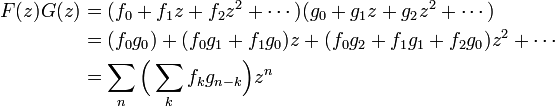Aritalab:Lecture/Basic/Generating Function
From Metabolomics.JP
< Aritalab:Lecture | Basic(Difference between revisions)
m |
m |
||
| Line 9: | Line 9: | ||
</math> | </math> | ||
| − | + | ==母関数の例== | |
| + | |||
| + | ===自然数=== | ||
| + | ''a<sub>n</sub>'' = ''n'' + 1 の母関数は | ||
| + | |||
| + | <math> | ||
| + | 1 + 2 z + 3 z^2 + \cdots = \Sigma^{\infty}_{n=0} (n+1)z^n | ||
| + | </math> | ||
| + | |||
| + | です。この右辺を閉じた式にするには | ||
| + | |||
| + | <math> | ||
| + | z(1 + z + z^2 + \cdots) = \Sigma^{\infty}_{n=0}z^{n+1} = z/(1-z) | ||
| + | </math> | ||
| + | |||
| + | が <math>|s| < 1</math> で収束するので、両辺を微分して | ||
| + | |||
| + | <math> | ||
| + | 1 + 2 z + 3 z^2 + \cdots = 1/(1-z)^2 | ||
| + | </math> | ||
| + | |||
| + | が得られます。 | ||
| + | |||
| + | ===べき乗=== | ||
| + | ''a<sub>n</sub>'' = 2<sup>''n''</sup>の母関数は | ||
| + | |||
| + | <math> | ||
| + | 1 + 2 z + 4 z^2 + \cdots = \Sigma^{\infty}_{n=0} (2z)^n = \frac{1}{1-2z} | ||
| + | </math> | ||
| + | |||
| + | です。ただし <math>|z| < 1/2 </math> と仮定します。 | ||
| + | |||
| + | ===二項定理=== | ||
| + | |||
| + | 二項定理は、<math>(1+z)^r</math> が数列<math>\textstyle \binom{r}{0}, \binom{r}{1}, \binom{r}{2}, \ldots </math>の母関数表現と解釈できます。すなわち | ||
<math> | <math> | ||
| − | + | \sum_{k=0}^{\infty} \binom{r}{k} z^k = (1+z)^r | |
</math> | </math> | ||
| − | + | が成立します。この式を二つ掛け合わせると | |
<math> | <math> | ||
| Line 21: | Line 55: | ||
</math> | </math> | ||
| − | 両者の Σ 式において ''z<sup>n</sup>'' | + | 両者の Σ 式において ''z<sup>n</sup>'' の係数が等しいとおけば |
<math> | <math> | ||
| Line 27: | Line 61: | ||
</math> | </math> | ||
| + | が得られます。これをヴァンデルモンドの畳み込み式 (convolution) といいます。 | ||
一般化すると以下のように書けます。 | 一般化すると以下のように書けます。 | ||
Revision as of 22:00, 25 May 2011
| Wiki Top | Up one level | レポートの書き方 | Arita Laboratory |
|
母関数
扱う対象とする無限列を、補助変数 z を用いてべき級数 (power series) として表現する方法を母関数 (generating function) といいます。
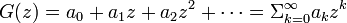
母関数の例
自然数
an = n + 1 の母関数は
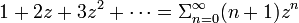
です。この右辺を閉じた式にするには
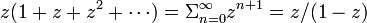
が 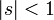 で収束するので、両辺を微分して
で収束するので、両辺を微分して
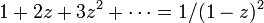
が得られます。
べき乗
an = 2nの母関数は
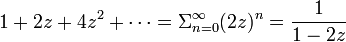
です。ただし 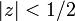 と仮定します。
と仮定します。
二項定理
二項定理は、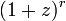 が数列
が数列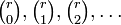 の母関数表現と解釈できます。すなわち
の母関数表現と解釈できます。すなわち
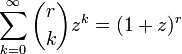
が成立します。この式を二つ掛け合わせると
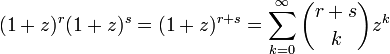
両者の Σ 式において zn の係数が等しいとおけば
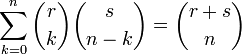
が得られます。これをヴァンデルモンドの畳み込み式 (convolution) といいます。 一般化すると以下のように書けます。